Đề thi thử trường THPT Thanh Chương 3 - Nghệ An lần 1
Cho
hàm số \[y=f\left( x \right)\]có đạo hàm liên tục trên khoảng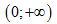 biết \[f'\left( x \right)+\left(
2x+3 \right){{f}^{2}}\left( x \right)=0,f\left( x \right)>0,\forall x>0\]
và \[f\left( 1 \right)=\frac{1}{6}.\]Tính giá trị của \[P=1+f\left( 1
\right)+f\left( 2 \right)+...+f\left( 2017 \right)\]
biết \[f'\left( x \right)+\left(
2x+3 \right){{f}^{2}}\left( x \right)=0,f\left( x \right)>0,\forall x>0\]
và \[f\left( 1 \right)=\frac{1}{6}.\]Tính giá trị của \[P=1+f\left( 1
\right)+f\left( 2 \right)+...+f\left( 2017 \right)\]
Trong không gian Oxyz, cho \[A\left( 0;0;-3 \right),\text{ }B\left( 2;0;-1 \right)\]và mp $\left( P \right):3x-8y+7z-1=0.$ Có bao nhiêu điểm C trên mặt phẳng (P) sao cho ABC đều.
Cho hàm số $y=f\left( x \right)\left( x-1 \right)$liên tục trên $\mathbb{R}$và có đồ thị như hình vẽ.
Tìm tất cả các giá trị của tham số m để phương trình $f\left( x \right)\left| x-1 \right|=m$ có số nghiệm lớn nhất.
Cho hàm số$y=f\left( x \right)$. Hàm số $y=f'\left( x \right)$có đồ thị như hình vẽ.

Hàm số $y=f\left( {{x}^{2}} \right)$ có bao nhiêu khoảng nghịch biến.
Cho hình lập phương \[ABCD.A'B'C'D'\]cạnh bằng a. Gọi K là trung điểm của DD'. Tính khoảng cách giữa hai đường thẳng CK và A’ D.
Cho hình chóp tứ giác đều \[S.ABCD\]các cạnh đáy bằng a, góc giữa cạnh bên SA và mặt đáy bằng ${{30}^{\circ }}$. Tính diện tích xung quanh ${{S}_{xq}}$ của hình trụ có một đường tròn đáy là đường tròn nội tiếp hình vuông ABCD và chiều cao bằng chiều cao của hình chóp \[S.ABCD\].
Có bao nhiêu giá trị nguyên của m để phương trình ${{4}^{{{x}^{2}}}}-{{3.2}^{{{x}^{2}}+1}}+m-3=0$ có 4 nghiệm phân biệt.
Tìm m để hàm số $f\left(
x \right)=-{{x}^{3}}-mx+\frac{3}{28{{x}^{7}}}$ nghịch biến 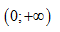
Cho hàm số $y={{x}^{3}}-3{{x}^{2}}$ có đồ thị $\left( C \right)$và điểm $A\left( 0;a \right)$. Gọi S là tập hợp tất cả các giá trị thực của a để có đúng hai tiếp tuyến của $\left( C \right)$ đi qua A . Tổng giá trị tất cả các phần tử của S bằng:
Cho hàm số $y={{x}^{3}}-3{{x}^{2}}$ có đồ thị $\left( C \right)$và điểm $A\left( 0;a \right)$. Gọi S là tập hợp tất cả các giá trị thực của a để có đúng hai tiếp tuyến của $\left( C \right)$ đi qua A . Tổng giá trị tất cả các phần tử của S bằng:
Cho số phức $z=a+bi\left( a,b\in \mathbb{R} \right)$thỏa mãn $\left( z+1+i \right)\left( \overline{z}-i \right)+3i=9$ và $\left| \overline{z} \right|>2.$Tính $P=a+b$.
Biết $\int\limits_{\frac{2\pi }{3}}^{\pi }{\frac{1-x\tan \,x}{{{x}^{2}}\cos x+x}dx=\ln \frac{\pi -a}{\pi -b}}\left( a;b\in \mathbb{Z} \right)$là. Tính $P=a+b$ ?
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d và mặt cầu (S) lần lượt có
phương trình là: $d:\frac{x+3}{-1}=\frac{y}{2}=\frac{z+1}{2};\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y+2z-18=0.$ Biết d cắt (S) tại hai điểm M, N thì độ dài đoạn MN là:
Cho hàm số $f\left( x \right)$xác định trên $\mathbb{R}\backslash \left\{ -1 \right\}$thỏa mãn $f'\left( x \right)=\frac{3}{x+1};f\left( 0 \right)=1$ và $f\left( 1 \right)+f\left( -2 \right)=2.$ Giá trị $f\left( -3 \right)$ bằng:
Cho hai số phức z; $\omega $ thỏa mãn \[\left| z-1
\right|=\left| z+3-2i \right|;\omega =z+m+i\] với \[m\in \mathbb{R}\] là tham số.
Giá trị của m để
ta luôn có  là:
là:
Trong không gian với hệ tọa độ Oxyz cho đường thăng \[\Delta :\frac{x}{1}=\frac{y-1}{1}=\frac{z-2}{-1}\] và mặt
phẳng \[\left( P \right):x+2y+2z-4=0.\] Phương trình đường thăng d nằm trong \[\left( P \right)\] sao cho d cắt và vuông góc với đường thẳng \[\Delta \] là:
Cho $f\left( x \right)=\left( {{m}^{4}}+1 \right){{x}^{4}}+\left( -{{2}^{m+1}}.{{m}^{2}}-4 \right){{x}^{2}}+{{4}^{m}}+16,m\in \mathbb{R}.$ Số cực trị của hàm số $y=\left| f\left( x \right)-1 \right|$ là:
Cho hình lăng trụ tứ giác đều $ABCD.{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}$ cạnh đáy bằng 1 và chiều cao bằng x. Tìm x để góc tạo bởi đường thẳng ${{B}_{1}}D$ và $\left( {{B}_{1}}{{D}_{1}}C \right)$ đạt giá trị lớn nhất.
Tìm m để giá trị lớn nhất của hàm số $y=\left| {{x}^{2}}+2x+m-4 \right|$ trên đoạn $\left[ -2;1 \right]$ đạt giá trị nhỏ nhất. Giá trị của m là:
Cho dãy số $\left( {{u}_{n}} \right)$ thỏa mãn $\log {{u}_{1}}+\sqrt{-2+\log {{u}_{1}}-2\log {{u}_{8}}}=2\log {{u}_{10}}$ và ${{u}_{n+1}}=10{{u}_{n}},\forall n\in {{\mathbb{N}}^{*}}.$ Khi đó ${{u}_{2018}}$ bằng:
Số hạng chứa ${{x}^{31}}$ trong khai triển ${{\left( x+\frac{1}{{{x}^{2}}} \right)}^{40}}$là:
Phần ảo của số phức $z=2-3i$là:
Cắt một hình nón bởi một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh bằng a. Tính thể tích của khối nón tương ứng.
Cho hai hàm số \[y=f\left( x \right)\text{ }v\grave{a}\text{ }y=g\left( x \right)\] liên tục trên đoạn $\left[ a;b \right].$ Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số đó và các đường thẳng $x=a,x=b$được tính theo công thức:
Tính $I=\int\limits_{0}^{lb2}{{{e}^{2x}}dx}$ ?
Cho đường thẳng $\Delta $ đi qua điểm $M\left( 2;0;-1 \right)$ và có vectơ chỉ phương $\overrightarrow{a}=\left( 4;-6;2 \right)$. Phương trình tham số của đường thẳng $\Delta $ là:
Cho hình chóp S.ABC đáy là tam giác đều cạnh a, hình chiếu vuông góc S lên đáy trùng với trung điểm BC và góc giữa SA và mặt phẳng đáy bằng ${{60}^{\circ }}.$Thể tích khối chóp S.ABC theo a là:
Cho hàm số $y=f\left( x \right)$có đồ thị như hình bên. Tìm mệnh đề sai trong các mệnh đề sau.

Khối 12 có 9 học sinh giỏi, khối 11 có 10 học sinh giỏi, khối 10 có 3 học sinh giỏi. Chọn ngẫu nhiên 2 học sinh trong số đó. Xác suất để 2 học sinh được chọn cùng khối.
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:

Hàm số $y=f\left( x \right)$ nghịch biến trên khoảng nào dưới đây?
Một tổ có 20 học sinh. Số cách chọn ngẫu nhiên 4 học sinh đi lao động là:
Khối đa diện bên dưới có bao nhiêu đỉnh?

Tập nghiệm của bất phương trình ${{3}^{3x}}\le {{3}^{x+2}}$ là:
Tìm nguyên hàm của hàm số \[f\left( x \right)={{e}^{x}}-{{e}^{-x}}\] ?
Số giao điểm của đồ thị hàm số \[y=\left( x-1 \right)\left( {{x}^{2}}-3x+2 \right)\] và trục hoành là:
Nếu $\log x=\frac{2}{3}\log a-\frac{1}{5}\log b$ thì x bằng:
Tìm giá trị lớn nhất của hàm số $f\left( x \right)={{x}^{4}}-2{{x}^{2}}+5$ trên đoạn $\left[ -2;2 \right]$ ?
Lập phương trình của mặt phẳng đi qua \[A\left( 2;6;-3 \right)\] và song
song với (Oyz).
Trong không gian Oxyz, mặt cầu tâm \[I\left( 1;2;3 \right)\] đi qua điểm \[A\left( 1;1;2 \right)\] có pt là:
Một người gửi vào ngân hàng 500 triệu đồng với lãi suất 0,6% một tháng, sau mỗi tháng lãi suất được nhập vào vốn. Hỏi sau một năm người đó rút tiền thì tổng số tiền người đó nhận được là bao nhiêu?
Hàm số $y=f\left( x \right)$ (có đồ thị như hình vẽ) là hàm số nào trong 4 hàm số sau?

Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ (T). Diện tích xung quanh ${{S}_{xq}}$ của hình trụ (T) là:
Đồ thị hàm số nào trong các hàm số dưới đây có tiệm cận đứng?
Cho số phức $u=3+4i$. Nếu ${{z}^{2}}=u$ thì ta có:
Giải phương trình ${{\log }_{2}}x.{{\log }_{3}}x+x.{{\log }_{3}}x+3={{\log }_{2}}x+3{{\log }_{3}}x+x.$ Ta có tổng các nghiệm là:
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng $\left(
P \right)$ đi qua hai điểm $A\left( 2;1;3 \right),B\left( 1;-2;1 \right)$và song
song với đường thẳng 
$\underset{x\to -\infty }{\mathop{\lim }}\,\frac{2x+1}{x-1}$bằng:
Phương trình \[cot3x=cotx\] có
mấy nghiệm thuộc  ?
?
Tứ diện đều ABCD cạnh a, M là trung điểm của CD. Côsin góc giữa AM và BD là:
Thể tích của khối nón có chiều cao h và bán kính đáy r là:
| 1 |
Minh13
Nguyễn Thị Minh
|
45/50
|
| 2 |
linh.colorfullife
Linh Nguyễn
|
44/50
|
| 3 |
eczacibasi
Nguyễn Pikachu
|
19/50
|
| 4 |
456876245327216
Kim Phượng
|
16/50
|
| 5 |
sangnguyen
Sang Nguyễn
|
4/50
|
| 6 |
honhuthuy1503
Hồ Như Thủy
|
1/50
|
| 7 |
vothiphuongvy171
Võ Thị Phương Vy
|
0/50
|
Đề thi thử trường THPT Thanh Chương 3 - Nghệ An lần 1
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm