Trần Trung Kiên

Cho hàm số \[f\left( x \right)\]liên tục trên $\mathbb{R}$ thỏa mãn \[\int\limits_{0}^{2018}{f\left( x \right)dx=2.}\] Khi đó giá trị của tích phân $I=\int\limits_{0}^{\sqrt{{{e}^{2018}}-1}}{\frac{x}{{{x}^{2}}+1}f\left( \ln \left( {{x}^{2}}+1 \right) \right)}\,dx$ bằng:

Tìm nguyên hàm $F\left( x \right)$ của hàm số $f\left( x \right)=\sin 2x$, biết $F\left( \frac{\pi }{6} \right)=0$.  

Cho hàm số $f\left( x \right)$ liên tục trên

và $\int\limits_{0}^{3}{f\left( \sqrt{x+1} \right)dx=8.}$ Tích phân $I=\int\limits_{1}^{2}{xf\left( x \right)dx}$ bằng:

Cho hàm số\[y=f(x)\]  liên tục trên đoạn \[\left[ 0;1 \right]\]và\[y={f}'(x)\] liên tục trên đoạn \[\left[ 0;1 \right]\], \[f(1)=4\]

Tính \[\int_{0}^{1}{\left[ {{x}^{2}}f(x)+\frac{{{x}^{3}}}{3}{f}'(x) \right]dx}\].

 Cho hàm số \[y=f\left( x \right)\] xác định trên \[\mathbb{R}\], thỏa mãn \[f\left( x \right)>0,\text{ }\forall x\in \mathbb{R}\] và \[f'\left( x \right)+2f\left( x \right)=0\]. Tính \[f\left( -1 \right)\], biết rằng \[f\left( 1 \right)=1\].

Xét hàm số $f\left( x \right)$ liên tục trên đoạn $\left[ 0;1 \right]$ và thỏa mãn $2f\left( x \right)+3f\left( 1-x \right)=\sqrt{1-{{x}^{2}}}.$ Tính $I=\int\limits_{0}^{1}{f\left( x \right)dx.}$

Cho hàm số $f\left( x \right)$ liên tục trên R và $f\left( x \right)\ne 0$ với mọi $x\in \text{R}\text{.}$ $f'\left( x \right)=\left( 2x+1 \right){{f}^{2}}\left( x \right)$ và $f\left( 1 \right)=-0,5.$ Biết rằng tổng $f\left( 1 \right)+f\left( 2 \right)+f\left( 3 \right)+...+f\left( 2017 \right)=\frac{a}{b};\,\left( a\in Z,b\in N \right)$ với $\frac{a}{b}$ tối giản. Mệnh đề nào dưới đây đúng ?

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -1;2 \right\}$ thỏa mãn $f'\left( x \right)=\frac{3}{{{x}^{2}}-x-2},f\left( -2 \right)=2\ln 2+2$ và $f\left( -2 \right)-2f\left( 0 \right)=4.$ Giá trị của biểu thức $f\left( -3 \right)+f\left( \frac{1}{2} \right)$ bằng:

 Biết tích phân $\int\limits_{0}^{\frac{\pi }{4}}{\frac{5\sin x+\cos x}{s\text{inx}+\cos x}dx}=a\pi +\ln b$ với a, b là các số hữu tỉ. Tính $S=a+b$.

 Cho hình phẳng \[\left( H \right)\] giới hạn bởi các đường \[y={{x}^{2}},\text{ }y=0,\text{ }x=0,\text{ }x=4.\] Đường thẳng \[y=k\text{ }\left( 0

Cho hàm số $y=f\left( x \right)$ xác định và liên tục trên $\mathbb{R}$ thỏa mãn đồ ng thời các điều kiện sau: 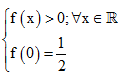   và $f'\left( x \right)=-{{e}^{x}}.{{f}^{2}}\left( x \right)$ với $\forall x\in \mathbb{R}.$ 

Cho tích phân $I=\int\limits_{0}^{\frac{\pi }{2}}{\frac{{{x}^{2}}+\left( 2\text{x}+\cos x \right)\cos x+1-\sin x}{x+\cos x}}d\text{x}=a{{\pi }^{2}}+b-\ln \frac{c}{\pi }.$ với a, b, c  là các số hữu tỉ. Tính giá trị của biểu thức $P=a{{c}^{3}}+b$. 

Cho các số thực a, b khác 0. Xét hàm số $f\left( x \right)=\frac{a}{{{\left( x+1 \right)}^{3}}}+bx{{e}^{x}}$ với $\forall x\ne -1.$ Biết \[f'\left( x \right)=f\left( 0 \right)=-22\text{ }\,v\grave{a}\text{ }\int\limits_{0}^{1}{f\left( x \right)dx=5}.\] Tính \[a+b\].

Cho hàm số \[y=f\left( x \right)\] liên tục trên \[\left[ 0;1 \right]\] thỏa mãn \[\int\limits_{0}^{1}{xf\left( x \right)dx}=0\] và \[\underset{\left[ 0;1 \right]}{\mathop{max}}\,\left| f\left( x \right) \right|=1.\] Tích phân \[I=\int\limits_{0}^{1}{{{e}^{x}}f\left( x \right)dx}\] thuộc khoảng nào trong các khoảng sau đây?

Tìm họ nguyên hàm $I=\int{\frac{9\cos x-5\sin x}{\cos x+\operatorname{s}\text{inx}}dx}.$ 

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và $f\left( x \right)+2f\left( \frac{1}{x} \right)=3x.$ Tính tích phân $I=\int\limits_{\frac{1}{2}}^{2}{\frac{f\left( x \right)}{x}dx.}$ 

Cho hàm số 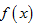liên tục trên 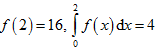. Tính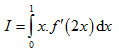

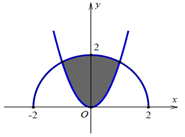
Cho (H) là hình phẳng giới hạn bởi parabol \[y=\sqrt{3}{{x}^{2}}\]và nửa đường tròn có phương trình \[y=\sqrt{4-{{x}^{2}}}\]với \[-2\le x\le 2\](phần tô đậm trong hình vẽ). Diện tích của (H) bằng

Biết $\int\limits_{1}^{2}{\frac{dx}{x\sqrt{x+1}+\left( x+1 \right)\sqrt{x}}}=\sqrt{a}-\sqrt{b}-\sqrt{c}$, với a, b, c là các số nguyên dương. Tính $P=a+b+c$.

Thể tích vật thể tròn xoay sinh ra khi hình phẳng giới hạn bới các đường $x=\sqrt{y};y=-x+2,x=0$ quanh trục Ox có giá trị là kết quả nào sau đây ?

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -1 \right\}$ thỏa mãn ${f}'\left( x \right)=\frac{3}{x+1};$ $f\left( 0 \right)=1$và $f\left( 1 \right)+f\left( -2 \right)=2$. Giá trị $f\left( -3 \right)$ bằng

Cho miền phẳng $\left( D \right)$ giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, hai đường thẳng $x=1,\,\,x=2$ và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay $\left( D \right)$quanh trục hoành.

Cho số thực $a>0$. Giả  sử hàm số $f\left( x \right)$ liên tục và luôn dương trên đoạn $\left[ 0;a \right]$ thỏa mãn $f\left( x \right).f\left( a-x \right)=1,\,\,\forall x\in \left[ 0;a \right].$ Tính tích phân $I=\int\limits_{0}^{a}{\frac{1}{1+f\left( x \right)}dx}.$

Cho hàm số $y=f\left( x \right)$ thỏa mãn $f'\left( x \right).f\left( x \right)={{x}^{4}}+{{x}^{2}}$. Biết $f\left( 0 \right)=2$. Tính ${{f}^{2}}\left( 2 \right).$

Biết \[\int\limits_{e}^{{{e}^{4}}}{f\left( \ln x \right)\frac{1}{x}dx}=4\]. Tính tích phân \[I=\int\limits_{1}^{4}{f\left( x \right)dx}\]

Cho hàm số $y=f\left( x \right)>0$ xác định, có đạo hàm trên đoạn $\left[ 0;1 \right]$ và thỏa mãn:

$g\left( x \right)=1+2018\int\limits_{0}^{x}{f\left( t \right)}dt,g\left( x \right)={{f}^{2}}\left( x \right).$ Tính $\int\limits_{0}^{1}{\sqrt{g\left( x \right)}d\text{x}}$ 

Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc $v\left( t \right)=7t\left( m/s \right).$ Đi được $5\left( s \right)$ người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \[a=-35\text{ }\left( m/{{s}^{2}} \right).\] Tính quãng đường của ô tô đi được tính từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.

Biết $\int\limits_{\frac{2\pi }{3}}^{\pi }{\frac{1-x\tan \,x}{{{x}^{2}}\cos x+x}dx=\ln \frac{\pi -a}{\pi -b}}\left( a;b\in \mathbb{Z} \right)$là. Tính $P=a+b$ ?

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên đoạn $\left[ 0;1 \right]$ và $f\left( 0 \right)+f\left( 1 \right)=0$. Biết $\int\limits_{0}^{1}{{{f}^{2}}\left( x \right)dx=\frac{1}{2},\int\limits_{0}^{1}{f'\left( x \right)c\text{os}\pi dx=\frac{\pi }{2}.}}$ Tính $\int\limits_{0}^{1}{f\left( x \right)dx}$

Biết \[\int{x\sqrt{{{x}^{2}}+1}}dx=\text{ }\frac{a}{b}({{x}^{2}}+1)\sqrt{{{x}^{2}}+1}+C\] (với a, b là các số nguyên dương và $\frac{a}{b}$ là phân số tối giản), khi đó giá trị của $b-a$  là:

Biết $\int{f\left( x \right)dx=2x\ln \left( 3x-1\right)+C}$ với  $x\in \left( \frac{1}{9};+\infty\right)$. Khẳng định nào sau đây đúng ?

Cho \[\int\limits_{\ln 2}^{1+\ln 2}{f\left( x \right)dx}=2018.\] Tính \[I=\int\limits_{1}^{e}{\frac{1}{x}f\left( \ln 2x \right)dx}.\]

Cho số dương a và hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn $f\left( x \right)+f\left( -x \right)=a\,\,\forall x\in \mathbb{R}$. Giá trị của biểu thức $\int\limits_{-a}^{a}{f\left( x \right)dx}$ bằng:

Cho biết $\int\limits_{1}^{2}{\ln \left( 9-{{x}^{2}} \right)dx=a\ln 5+b\ln 2+c}$, với a, b, c là các số nguyên. Tính $S=\left| a \right|+\left| b \right|+\left| c \right|$ được:

Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số \[y=\sqrt{x}\], trục hoành và đường thẳng \[x=9.\] Khi (H) quay quanh trục Ox tạo thành một khối tròn xoay có thể tích bằng:

Cho hàm số \[f(x)\] liên tục trên \[\mathbb{R}\] và có \[\int\limits_{0}^{1}{f(x)dx=2};\]\[\int\limits_{0}^{3}{f(x)dx=6}\]. Tính \[I=\int\limits_{-1}^{1}{f(|2x-1|)dx.}\]

Xét hàm số $f\left( x \right)$ liên tục trên đoạn $\left[ 0;1 \right]$ và thỏa mãn $2f\left( x \right)+3f\left( 1-x \right)=\sqrt{1-x}.$ Tích phân $\int\limits_{0}^{1}{f\left( x \right)dx}$ bằng:

Cho hàm số $y=f\left( x \right)$liên tục trên $\mathbb{R}$ và là hàm số chẵn, biết $\int\limits_{-1}^{1}{\frac{f\left( x \right)}{1+{{e}^{x}}}}d\text{x}=1.$ Tính$\int\limits_{-1}^{1}{f\left( x \right)}d\text{x}$ 

Cho hàm số $f\left( x \right)$ liên tục và nhận giá trị dương trên $\left[ 0;1 \right]$. Biết $f\left( x \right).f\left( 1-x \right)=1$ mọi x thuộc $\left[ 0;1 \right]$. Tính giá trị $I=\int\limits_{0}^{1}{\frac{dx}{1+f\left( x \right)}}$.

Cho $f\left( x \right)$ liên tục trên $\mathbb{R}$ và $f\left( 2 \right)=16,\int\limits_{0}^{1}{f\left( 2x \right)dx=2.}$ Tích phân $\int\limits_{0}^{2}{xf'\left( x \right)dx}$ bằng: