Đề thi thử THPT Quỳnh Lưu 1 - Nghệ An - Lần 2
Cho tập $M=\left\{ 1;\text{ }2;\text{ }3;\text{ }4;\text{ }5;\text{ }6;\text{ }7;\text{ }8;\text{ }9 \right\}$. Số các số tự nhiên gồm 4 chữ số phân biệt lập từ $M$ là
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau

Hàm số $y=f\left( x \right)$ đồng biến trên khoảng nào dưới đây?
Một hộp đựng 10 thẻ được đánh số từ 1 đến 10. Phải rút ra ít nhất k thẻ để xác suất có ít nhất một thẻ ghi số chia hết cho 4 lớn hơn \[\frac{13}{15}\]. Giá trị của k bằng
Trong không gian $Oxyz$, cho điểm $A\left( 3;\,-4;\,5 \right)$. Hình chiếu vuông góc của $A$ trên mặt phẳng $\left( Oxz \right)$ là điểm
Gọi A, B là hai điểm biểu diễn hai nghiệm phức của phương trình ${{z}^{2}}+2z+5=0$. Tính độ dài đoạn thẳng AB
Biết $\int\limits_{-\frac{\pi }{6}}^{\frac{\pi }{6}}{\frac{x\cos x}{\sqrt{1+{{x}^{2}}}+x}\text{d}x}=a+\frac{{{\pi }^{2}}}{b}+\frac{\sqrt{3}\pi }{c}$với $a,\ b,\ c$ là các số nguyên. Tính $M=a-b+c$.
Trong không gian $Oxyz$,cho ba điểm $M\left( 3;0;0 \right)$,$N\left( 0;-2;0 \right)$ và $P\left( 0;0;1 \right)$. Mặt phẳng $\left( MNP \right)$ có phương trình là
Trong không gian $Oxyz$, cho hai điểm $A\left( -2\,;\,3\,;\,2 \right)$ và $B\left( 2\,;\,1\,;\,0 \right)$. Mặt phẳng trung trực của $AB$ có phương trình là
Đồ thị hàm số nào dưới đây có tiệm cận đứng?
Tập nghiệm của bất phương trình ${{4}^{x}}>{{2}^{x+8}}$ là
Cho hình trụ có diện tích xung quanh bằng $2\pi {{a}^{2}}$ và bán kính đáy bằng $a$. Độ dài đường sinh của hình trụ đã cho bằng
Giá trị nhỏ nhất của hàm số \[y=\frac{x-1}{x+1}\] trên đoạn $\left[ 0;3 \right]$ là:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f(x)$, $y=g(x)$ liên tục trên đoạn \[\left[ a;b \right]\] và hai đường thẳng $x=a$, $x=b$ được xác định theo công thức
Với $a$ là số thực dương bất kì, mệnh đề nào sau đây đúng?
Họ nguyên hàm của hàm số $f\left( x \right)=2{{x}^{2}}+x+1$ là
Cho khối chóp \[S.ABCD\] có thể tích bằng $\sqrt{3}.{{a}^{3}}$. Mặt bên \[SAB\] là tam giác đều cạnh a và thuộc mặt phẳng vuông góc với đáy, biết đáy ABCD là hình bình hành. Tính theo a khoảng cách giữa SA và CD.
Trong không gian \[Oxyz\], cho mặt phẳng $(P):2x-z+1=0$. Mặt phẳng $(P)$ có một vectơ pháp tuyến là
Số giá trị $m$ nguyên trên $\left[ -2;2018 \right]$ để hàm số $y={{e}^{{{x}^{3}}-{{x}^{2}}+mx}}$ đồng biến trên $\left[ 1,2 \right]$.
Cho hàm số \[y=f(x)\] có bảng biến thiên như sau:Đồ thị hàm số \[y=\frac{1}{f(3-x)-2}\] có bao nhiêu tiệm cận đứng.
Cho số phức \[z=-2+i\]. Điểm nào dưới đây là điểm biểu diễn của số phức \[w=iz\] trên mặt phẳng tọa độ ?
Thầy Châu vay ngân hàng ba trăm triệu đồng theo phương thức trả góp để mua xe. Nếu cuối mỗi tháng, bắt đầu từ tháng thứ nhất thầy Châu trả 5 triệu đồng và chịu lãi số tiền chưa trả là 0,65% mỗi tháng (biết lãi suất không thay đổi) thì sau bao lâu thầy Châu trả hết số tiền trên?
Giới hạn \[\underset{x\to -\infty }{\mathop{\lim }}\,\frac{x-\sqrt{{{x}^{2}}+x}}{x+1}\] bằng
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau
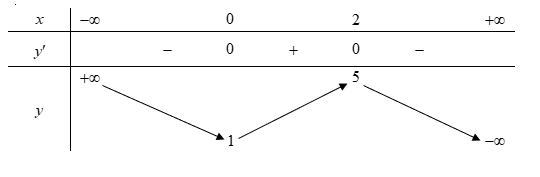
Hàm số $y=2f(x)+1$ đạt cực tiểu tại điểm
Thể tích của khối nón có chiều cao bằng $h$ và bán kính đáy bằng $R$ là
Tìm hệ số của ${{x}^{5}}$trong khai triển thành đa thức của ${{(2-3x)}^{2n}}$, biết n là số nguyên dương thỏa mãn : $C_{2n+1}^{0}+C_{2n+1}^{2}+C_{2n+1}^{4}+...+C_{2n+1}^{2n}=1024$.
Số nghiệm của phương trình: ${{\log }_{4}}\left( {{\log }_{2}}x \right)+{{\log }_{2}}\left( {{\log }_{4}}x \right)=2$ là:
Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên như sau
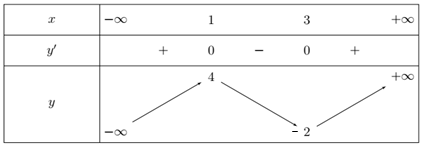
Phương trình \[f\left( x \right)-2m=0\] có 3 nghiệm khi
Trong không gian $Oxyz,$ cho mặt phẳng \[\left( P \right):x-2y+2z-5=0\] và hai điểm \[A\left( -3;0;1 \right),\text{ }B\left( 1;-1;3 \right).\] Trong các đường thẳng đi qua \[A\] và song song với \[\left( P \right)\], đường thẳng mà khoảng cách từ \[B\] đến đường thẳng đó là nhỏ nhất có phương trình là.
Đường cong trong hình bên dưới là đồ thị của hàm số nào dưới đây?

Cho hình chóp tứ giác đều có cạnh đáy bằng \[a\sqrt{2}\] và chiều cao bằng \[\frac{a\sqrt{2}}{2}\]. Tang của góc giữa mặt bên và mặt đáy bằng:
Tích phân \[\int\limits_{0}^{2}{\frac{x\text{d}x}{{{x}^{2}}+3}}\] bằng
Trong một chiếc hộp hình trụ người ta bỏ vào đó ba quả bóng tennis, biết rằng đáy của hình trụ bằng hình tròn lớn trên quả bóng và chiều cao của hình trụ bằng 3 lần đường kính của quả bóng. Gọi ${{S}_{1}}$ là tổng diện tích của ba quả bóng và ${{S}_{2}}$ là diện tích xung quanh của hình trụ. Giá trị biểu thức ${{2018}^{\frac{{{S}_{1}}}{{{S}_{2}}}}}$ bằng:
Các giá trị của \[m\] để phương trình ${{\left( \sqrt{5}-1 \right)}^{{{x}^{2}}}}+m{{\left( \sqrt{5}+1 \right)}^{{{x}^{2}}}}={{2}^{{{x}^{2}}-2}}$ có đúng bốn nghiệm phân biệt là khoảng $(a;b)$. Giá trị $b-a$ là
Cho hình chóp \[S.ABCD\] có tất cả các cạnh đều bằng\[~a\]. Gọi \[I\] và \[J\] lần lượt là trung điểm của \[SC\] và \[BC\]. Số đo của góc \[\left( \text{ }IJ,\text{ }CD \right)\] bằng:
Thể tích $V$của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đường tròn $(C):{{x}^{2}}+{{(y-3)}^{2}}=1$ xung quanh trục hoành là
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $B$,$AB=a,AB=a,SA=2a$ và \[SA\bot \left( ABC \right)\]. Gọi $H,K$ lần lượt là hình chiếu vuông góc của $A$ lên $SB,SC$. Tính thể tích tứ diện $S.AHK$
Cho hàm số $f(x)$ có đạo hàm$f'(x)={{(x+1)}^{4}}{{(x-m)}^{5}}{{(x+3)}^{3}}$. Có bao nhiêu giá trị nguyên của tham số m trong đoạn$\left[ -5;5 \right]$ để số điểm cực trị của hàm số$f(\left| x \right|)$ bằng $3$:
Giả sử ${{z}_{1}},{{z}_{2}}$ là hai nghiệm phức của phương trình \[\left| \left( 2+i \right)\left| z \right|z-(1-2i)z \right|=\left| 1+3i \right|\] và $\left| {{z}_{1}}-{{z}_{2}} \right|=1$. Tính $M=\left| 2{{z}_{1}}+3{{z}_{2}} \right|$
Trong tất cả các số phức z thỏa mãn điều kiện sau: $\left| z+1 \right|=\left| \frac{z+\overline{z}}{2}+3 \right|$, gọi số phức $z=a+bi$ là số phức có môđun nhỏ nhất. Tính $S=2a+b.$
Trong hệ tọa độ Oxyz cho\[A(3,3,0),B(3,0,3),C(0,3,3)\]. Mặt phẳng (P) đi qua O, vuông góc với mặt phẳng (ABC) sao cho mặt phẳng (P) cắt các cạnh AB, AC tại các điểm M, N thỏa mãn thể tích tứ diện OAMN nhỏ nhất. Mặt phẳng (P) có phương trình:
Có bao nhiêu giá trị nguyên m để phương trình \[{{(8{{\sin }^{3}}x-m)}^{3}}=162\sin x+27m\] có nghiệm thỏa mãn \[0
Một khúc gỗ có dạng hình khối nón có bán kính đáy bằng \[r=2m\], chiều cao \[h=6m\]. Bác thợ mộc chế tác từ khúc gỗ đó thành một khúc gỗ có dạng hình khối trụ như hình vẽ. Gọi \[V\] là thể tích lớn nhất của khúc gỗ hình trụ sau khi chế tác. Tính \[V\].

Trong không gian với hệ trục toạ độ $Oxyz$, cho mặt cầu $\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=9$, điểm $A\left( 0;0;2 \right)$. Phương trình mặt phẳng $\left( P \right)$ đi qua $A$ và cắt mặt cầu $\left( S \right)$ theo thiết diện là hình tròn $\left( C \right)$có diện tích nhỏ nhất là:
Gọi ${{x}_{1}},\text{ }{{x}_{2}}$ lần lượt là cực đại và cực tiểu của hàm số $f\left( x \right)=\int\limits_{{{e}^{x}}}^{{{e}^{2x}}}{t\ln tdt}$. Tính $S={{x}_{1}}+{{x}_{2}}$ .
Cho hàm số $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ
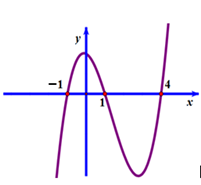 Hàm số $y=f\left( 3-2x \right)+2018$ nghịch biến trên khoảng
Hàm số $y=f\left( 3-2x \right)+2018$ nghịch biến trên khoảng
Cho hàm số $y={{x}^{3}}-2{{x}^{2}}+(m-1)x+2m$ có đồ thị là $({{C}_{m}})$. Tìm $m$ để tiếp tuyến có hệ số góc nhỏ nhất của đồ thị $({{C}_{m}})$ vuông góc với đường thẳng $\Delta :y=3x+2018$.
Có bao nhiêu số tự nhiên có 2018 chữ số sao cho trong mỗi số tổng các chữ số bằng 5?
Cho hàm số \[f\left( x \right)\ne 0\] thỏa mãn điều kiện \[{f}'\left( x \right)=\left( 2x+3 \right){{f}^{2}}\left( x \right)\] và \[f\left( 0 \right)=-\frac{1}{2}.\]
Biết rằng tổng \[f\left( 1 \right)+f\left( 2 \right)+f\left( 3 \right)+\,\,...\,\,+f\left( 2017 \right)+f(2018)=\frac{a}{b}\] với \[\left( a\in \mathbb{Z},\,\,b\in {{\mathbb{N}}^{*}} \right)\] và \[\frac{a}{b}\] là phân số tối giản. Mệnh đề nào sau đây đúng?
Cho dãy số $\left( {{u}_{n}} \right)$ thỏa mãn $\ln ({{u}_{1}}^{2}+{{u}_{2}}^{2}+10)=\ln (2{{u}_{1}}+6{{u}_{2}})$ và ${{u}_{n+2}}+{{u}_{n}}=2{{u}_{n+1}}+1$ với mọi $n\ge 1$. Giá trị nhỏ nhất của $n$ để ${{u}_{n}}>5050$ bằng
Trong không gian với hệ tọa độ $Oxyz$cho các điểm $A(2;0;0);B(0;3;0);C(0;0;6);D(1;1;1)$. Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm$O,A,B,C,D$?
| 1 |
htya8k71lnqhero
Yến Hoàng
|
31/50
|
| 2 |
minhtri
Dương Minh Trí
|
30/50
|
| 3 |
coolkidoverr
Trần Thảo
|
18/50
|
| 4 |
vutriphuong2701
tri phuong vu thi
|
17/50
|
| 5 |
thonguyenduy
thonguyenduy
|
16/50
|
| 6 |
phamngocquang10a1
Ngoc Quang
|
16/50
|
| 7 |
phamnguyennganha1522001
Ngan Ha Pham
|
13/50
|
| 8 |
thaituhongphuc
Phúc Nguyên Hồng
|
13/50
|
| 9 |
anhthu180102
Ant Nguyễn
|
12/50
|
| 10 |
496375827969291
Cậu Út Làng Đại
|
11/50
|
| 11 |
lehang.dhyhn
Hằng Lê
|
11/50
|
| 12 |
nguyetdo201
Nguyet Anh
|
9/50
|
| 13 |
Vuduc6677
Vũ văn đức
|
9/50
|
| 14 |
xuanhuy900
Xuân Huy
|
8/50
|
| 15 |
507029076502413
Bao Nguyen
|
5/50
|
| 16 |
vttiem12
Tran quoc cuong
|
4/50
|
| 17 |
thao123
thảo
|
2/50
|
| 18 |
z21032001
Hoàng Phong
|
2/50
|
| 19 |
vuthihiendiu
Lộc Linh
|
2/50
|
| 20 |
le.kangmi01
Như Mơ
|
1/50
|
| 21 |
catan271
Trần Đức Cảnh
|
1/50
|
| 22 |
ngoctuyet23102002
Ngọc Tuyết
|
1/50
|
| 23 |
tranthuhuongtq2002
Hường Trần Thu
|
1/50
|
| 24 |
vietanhmonster12
Việt Anh Vũ
|
0/50
|
| 25 |
c2daotu.tamduong
Đạo Tú Trường THCS
|
0/50
|
| 26 |
pubi123
Alaa
|
0/50
|
| 27 |
123456000
Trâm Bảo
|
0/50
|
| 28 |
lol1234
Lola
|
0/50
|
| 29 |
tungnx82
Ngô Văn Đình
|
0/50
|
| 30 |
maihuyloga12
trịnh mai huy
|
0/50
|
Đề thi thử THPT Quỳnh Lưu 1 - Nghệ An - Lần 2
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm