chậc 12345 hehehe

Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y=\frac{x-2}{{{x}^{2}}-m\text{x}+1}$ có hai đường tiệm cận đứng.

Chất X có công thức phân tử C2H7O3N. Khi cho X tác dụng với dung dịch HC1 hoặc dung dịch NaOH đun nóng nhẹ đều thấy khí thoát ra. Lấy 0,1 mol X cho vào dung dịch chứa 0,25 mol KOH. Sau phản ứng cô cạn dung dịch được chất rắn Y, nung nóng Y đến khối lượng không đổi được m gam chất rắn. Giá trị của m là:

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y={{x}^{3}}-3{{x}^{2}}-9x+40\] trên đoạn \[\left[ -5;5 \right]\] lần lượt là:

Để khử mùi tanh của cá (gây ra do một số amin), ta có thể rửa cá với

Cho hàm số $y=f\left( x \right)$ có bảng thiến thiên như sau:

Hàm số đạt cực tiểu tại điểm nào?

Số tiếp tuyến kẻ từ diểm $A\left( 1;5 \right)$ tới đồ thị hàm số $y=-{{x}^{3}}+6x$ là:

Đồ thị hàm số nào sau đây không có tiệm cận ngang ?

Chất hữu cơ X có công thức phân tử C3H9O2N. Cho 9,1 gam X tác dụng với dung dịch NaOH vừa đủ. Cô cạn dung dịch sau phản ứng thu được 6,8 gam chất rắn khan. Số công thức cấu tạo của X phù hợp với tính chất trên là

Tristearin tác dụng với chất (hoặc dung dịch) nào sau đây ?

Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực trị?

Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng ? 

Cho hàm số $f\left( x \right)=\operatorname{s}\text{inx}-cos\text{x+2x}\text{.}$ Khẳng định nào sau đây là đúng ?

Hàm số \[y=\left| x \right|\] có bao nhiêu điểm cực trị ?

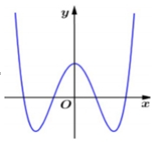
Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là đúng? 

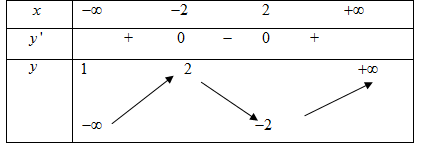
Giá trị cực tiểu của hàm số $y={{x}^{3}}-3{{x}^{2}}-9x+2$ là:

Cho hàm số \[y=f\left( x \right)\] có \[f'\left( x \right)=\left( 2x-1 \right){{x}^{2}}{{\left( 1-x \right)}^{2}}.\] Khẳng định nào sau đây là khẳng định đúng ?

Phương trình tiếp tuyến của đồ thị hàm số $y=x+\sqrt{{{x}^{2}}+1}$ tại điểm có hoành độ $x=0$ là:

Cho sơ đồ phản ứng:

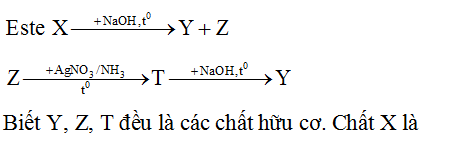
Đồng phân của glucozo là

Hàm số nào sau đây có ba điểm cực trị ?

Đồ thị sau đây là của hàm số nào ?

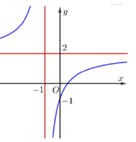
Cho hàm $y=f(x)$ số xác định trên $\mathbb{R}\backslash \left\{ \pm 1 \right\},$ liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau.

Tìm tập hợp tất cả các giá trị của tham số m để phương trình $f\left( x \right)=m$ vô nghiệm.

Hàm số nào sau đây đồng biến trên\[\left( -\infty ;+\infty \right)\] ?

Gọi ${{y}_{CD}},{{y}_{CT}}$ lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số $y=\frac{{{x}^{2}}+3x+3}{x+2}$. Gía trị của biểu thức $y_{CD}^{2}-2y_{CT}^{2}$ bằng

Một động cơ điện xoay chiều hoạt động bình thường với điện áp hiệu dụng bằng 200 V và cường độ dòng điện hiệu dụng bằng 0,5 A. Nếu công suất tỏa nhiệt trên dây quấn là 8W và hệ số công suất của động cơ là 0,8 thì hiệu suất của động cơ là

Biết rằng đường thẳng \[d:y=3x+m\] (với m là số thực) tiếp xúc với đồ thị hàm số

\[\left( C \right):y={{x}^{2}}-5x-8.\]Tìm tọa độ tiếp điểm của d và (C) .

Tìm tất cả các giá trị của tham số m để hàm số $y=-{{x}^{4}}+\left( m-2 \right){{x}^{2}}+4$ có ba điểm cực trị.

Đường tiệm cận đứng của đồ thị hàm số $y=\frac{2-x}{x+2}$ có phương trình là:

Số điểm cực trị của hàm số $y={{x}^{4}}+100$ là:

Cho hàm số có đồ thị \[y=f\left( x \right)\]như dưới đây. Hãy chỉ ra giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn\[\left[ -2;3 \right]\].