tổng ôn môn toán

Cho hàm số có đồ thị ( C ). Số tiếp tuyến với đồ thị (C) song song với đường thẳng là

Cho ba hình tam giác đều cạnh bằng a chồng lên nhau như hình vẽ (cạnh đáy của tam giác trên đi qua các trung điểm hai cạnh bên của tam gác dưới). Tính theo a thể tích của khối tròn xoay tạo thành khi quay chúng xung quanh đường thẳng (d).

Gọi $A,\,\,B$ là hai điểm cực trị của đồ thị hàm số $f(x)={{x}^{3}}-3{{x}^{2}}+m$ với $m$là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số $m$để trọng tâm tam giác $OAB$ thuộc đường thẳng $3x+3y-8=0$.

Cho hàm số \[y={{x}^{3}}-3x+2\] có đồ thị \[\left( C \right)\]. Gọi d là đường thẳng đi qua điểm A(3;20) và có hệ số góc là m. Với giá trị nào của m thì d cắt \[\left( C \right)\] tại 3 điểm phân biệt

Một cái phễu có dạng hình nón, chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng 10 cm. Nếu bịt kín miệng phễu và lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng nhất với giá trị nào sau đây.

Cho tam giác ABC với \[A\left( 2;-3;2 \right),\text{ B}\left( 1;-2;2 \right),\text{ C}\left( 1;-3;3 \right).\] Gọi A’, B’, C’ lần lượt là hình chiếu vuông góc của A, B, C lên mặt phẳng 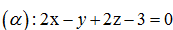Khi đó, diện tích tam giác A’B’C’ bằng:

 Số nghiệm của phương trình $\frac{{{x}^{2}}}{2}+x-\ln \left( {{x}^{2}}-2 \right)=2018$ là:

Hãy lập phương trình đường thẳng (d) đi qua các điểm cực đại và cực tiểu của đồ thị hàm số \[y={{x}^{3}}+3m{{x}^{2}}-3x\].

Cho hàm số \[f(x)={{\ln }^{2}}({{x}^{2}}-2x+4)\]. Tìm các giá trị của x để \[f'(x)>0.\]

Cho hàm số $y=f(x)$ xác định và liên tục trên $\mathbb{R}$  có  $f(x)>0\text{ }\forall x\in \mathbb{R}$, $f(0)=1$ Biết $\frac{f'(x)}{f(x)}=2-2x$, tìm tất cả các giá trị của m để phương trình $f(x)=m$ có 2 nghiệm thực phân biệt.

Cho các số phức z và w thỏa mãn \(\left( {3 - i} \right)\left| z \right| = \frac{z}{{w - 1}} + 1 - i\). Tìm GTLN của \(T = \left| {w + i} \right|\).

Cho hai số phức \({z_1},{z_2}\) khác \(0\) thỏa mãn \(\dfrac{{{z_1}}}{{{z_2}}}\) là số thuần ảo và \(\left| {{z_1} - {z_2}} \right| = 10\). Giá trị lớn nhất của \(\left| {{z_1}} \right| + \left| {{z_2}} \right|\) bằng