chậc 12345 hehehe

Gọi S là tập hợp các giá trị thực của tham số m để hàm số $y={{x}^{3}}-3m{{x}^{2}}+4{{m}^{3}}$ có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 (O là gốc tọa độ). Ta có tổng giá trị tất cả các phần tử của tập S bằng:

C4H8O2 có số đồng phân este là:

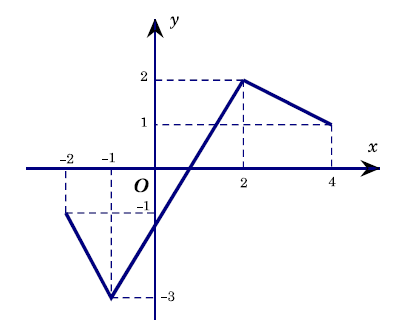
Cho hàm số \[y=f\left( x \right)\] có đồ thị trên đoạn \[\left[ -2;4 \right]\] như hình vẽ. Tìm giá trị lớn nhất của hàm số \[y=\left| f\left( x \right) \right|\] trên đoạn \[\left[ -2;4 \right]\]

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:

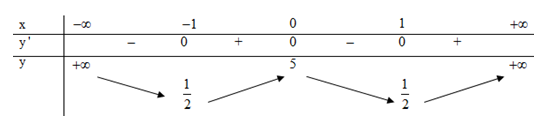
Số nghiệm của phương trình $f\left( x \right)-6=0$ là

Cho hàm số $y=f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -1 \right\},$ liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau :

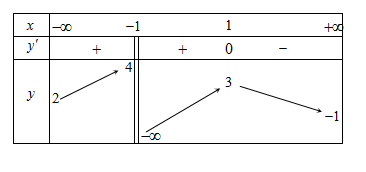
Khẳng định nào dưới đây sai ?

Cho hàm số $y=\ln x.$ Mệnh đề nào dưới đây đúng ?

Lượng glucozơ cần dùng để tạo ra 1,82 gam sobitol với hiệu suất 80% là

Tìm tất cả các giá trị của m để phương trình \[{{x}^{4}}-2{{x}^{2}}-m=0\] có bốn nghiệm phân biệt. 

Cho hàm số $y=\frac{1}{4}{{x}^{4}}-2{{x}^{2}}+3$. Khẳng định nào sau đây đúng ?

Hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng ?

Đa diện đều loại \[\left\{ 5,3 \right\}\] có tên gọi nào dưới đây ?

Tính tổng số đỉnh và số mặt của khối đa diện đều loại $\left\{ 5;3 \right\}$

Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng ?

Hình lăng trụ có thể có số cạnh là số nào sau đây ?

Chọn khẳng định sai. Trong một khối đa diện:

 Tìm tất cả các giá trị thực của m để đồ thị hàm số $y={{x}^{4}}-8{{m}^{2}}{{x}^{2}}+1$ có ba điểm cực trị đồng thời ba điểm cực trị đó là ba đỉnh của một tam giác có diện tích bằng $64$.

Cho đồ thị $\left( C \right):{{x}^{3}}-3{{x}^{2}}.$ Có bao nhiêu số nguyên $b\in \left( -10;10 \right)$ để có đúng một tiếp tuyến của $\left( C \right)$ đi qua điểm $B\left( 0;b \right)?$

Cho hàm số $y=\frac{x-1}{2x-3}.$ Gọi I là giao điểm của hai tiệm cận của đồ thị hàm số. Khoảng cách từ I đến tiếp tuyến của đồ thị hàm số đã cho đạt giá trị lớn nhất bằng:

Cho hàm số $y={{x}^{3}}-3x$ có đồ thị $\left( C \right).$ Gọi S là tập hợp tất cả các giá trị thực của k để đường thẳng $y=k\left( x+1 \right)+2$ cắt đồ thị $\left( C \right)$ tại ba điểm phân biệt \[M\text{ }\left( -1;2 \right),\text{ }N,\text{ }P\] sao cho các tiếp tuyến của $\left( C \right)$ tại N và P vuông góc với nhau. Tính tích tất cả các phần tử của tập S.

Có bao nhiêu giá trị nguyên của tham số m để hàm số \[y=\text{ }\left| {{x}^{4}}-\text{ }8{{x}^{3}}+\text{ }18{{x}^{2}}+m \right|\] có 3 điểm cực trị ?