chậc 12345 hehehe

Trong các khẳng định sau về hàm số $y=-2{{x}^{4}}+4{{x}^{2}}-1,$ khẳng định nào là SAI ?

Hàm số $y=\text{a}{{\text{x}}^{3}}+b{{x}^{2}}+cx+d$ với $a,b,c,d$ là các số thực và $a\ne 0$ có tối đa bao nhiêu điểm cực trị ?

Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y={{x}^{3}}+{{x}^{2}}-\left( 2m+1 \right)x+4$ có đúng hai cực trị. 

Đồ thị hàm số $y={{x}^{3}}+3{{x}^{2}}-9x-1$ có hai cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB

Cho hàm số \[y=-{{x}^{3}}+3{{x}^{2}}+1\]. Chọn khẳng định đúng trong các khẳng định sau.

Lên men m gam glucozơ với hiệu suất 90%, lượng khí CO2 sinh ra hấp thụ hết vào dung dịch nước vôi trong thu được 10 gam kết tủa. Khối lượng dung dịch sau phản ứng giảm 3,4 gam so với khối lượng dung dịch nước vôi trong ban đầu. Giá trị của m là:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số \[y=\frac{{{x}^{2}}+m}{{{x}^{2}}-3x+2}\] có đúng hai đường tiệm cận.

Tập hợp tất cả các giá trị của tham số m để đường thẳng $y=-2x+m$ tiếp xúc với đồ thị hàm số $y=\frac{x+1}{x-1}$ là:

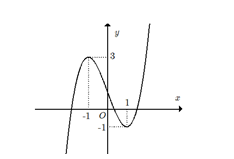
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

\

Tìm m để hàm số $y=-{{x}^{3}}+m\text{x}$ nghịch biến trên $\mathbb{R}$.

Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên sau

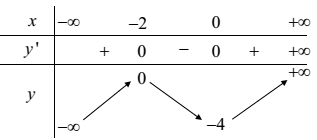
                 Số nghiệm của phương trình \[f\left( x \right)+3=0\] là

Gọi A là tập hợp các giá trị của tham số m sao cho hàm số $y={{x}^{3}}-3{{x}^{2}}+\left( {{m}^{2}}-2m \right)x-1$ có hai điểm cực trị ${{x}_{1}},\,{{x}_{2}}$ thỏa \[x_{1}^{2}+x_{2}^{2}=2.\] Số phần tử của tập hợp A là

 

Cho hàm số $f\left( x \right)$liên tục trong đoạn $\left[ 1;e \right]$, biết $\int\limits_{1}^{e}{\frac{f\left( x \right)}{x}dx}=1,f\left( e \right)=2.$ Tích phân $\int\limits_{1}^{e}{f'\left( x \right)\ln xdx}=?$ 

Nghiệm của bất phương trình là

Cho hàm số $y=\frac{x+3}{x+1}\left( C \right)$. Đường thẳng $d:y=2x+m$ cắt (C) tại 2 điểm phân biệt M, N và MN nhỏ nhất khi

Cho hàm số \[f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\] thỏa mãn \[a,b,c,d\in \mathbb{R}\];\[a>0\] và . Số cực trị của hàm số \[y=\left| f\left( x \right)-2019 \right|\] bằng:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}-mx+2$ có hai điểm cực trị A và B sao cho các điểm A, B và $M\left( 0;3 \right)$ thẳng hàng.

Đường cong ở hình dưới là đồ thị của một trong bốn hàm số ở dưới đây. Hàm số đó là hàm số nào?

Cho hàm số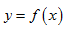xác định trên và có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để phương trình 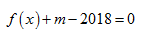có duy nhất một nghiệm. 

Một trong các đồ thị ở hình vẽ là đồ thị của hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn $f'\left( 0 \right)=0,f''\left( x \right)