Đề 1 21321321321

Đồ thị hàm số \[y={{x}^{3}}+2x-1\]cắt đồ thị hàm số \[y={{x}^{2}}-3x+1\] tại hai điểm phân biệt. Tình độ dài đoạn AB.

Cho đồ thị hàm số \[\left( C \right): y={{x}^{3}}-3x\]. Mệnh đề nào dưới đây sai ? 

Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng AB = 5 km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7km. Người canh hải đăng có thể chèo đò từ A đến điểm D  trên biển với vận tốc 4km/h rồi đi bộ đến C vơi vận tốc 6km/h. Xác định khoảng cách từ D đến B để người đó đến kho nhanh nhất.

Tổng số hợp chất hữu cơ no, đơn chức, mạch hở có cùng công thức phân tử C5H10O2, phản ứng được với dung dịch NaOH nhưng không có phản ứng tráng bạc là

Mệnh đề nào dưới đây sai ?

Cho đồ thị (C): $y\,=\,{{x}^{4}}\,-\,2{{\text{x}}^{2}}$. Khẳng định nào sau đây là sai ?

Tìm các khoảng đồng biến của hàm số $y=2{{x}^{5}}-\frac{10}{3}{{x}^{3}}+1.$ 

Hàm số nào sau đây nghịch biến trên tập $\mathbb{R}$ ?

Gọi \[\left( C \right)\] là đồ thị hàm số \[y={{x}^{3}}-3x+3\]. Khẳng định nào sau đây là sai?

Hàm số $y=\frac{2}{2+{{x}^{2}}}$ đồng biến trên khoảng nào dưới đây ?

Cho hàm số: \[y-\left( 1-m \right){{x}^{4}}-m{{x}^{2}}+2m-1\] . Tìm \[m\] để đồ thị hàm số có đúng một cực trị.

Trong các hàm số sau , hàm số nào đồng biến trên $\mathbb{R}$ .

Cho các phát biểu sau:

(a) Hiđro hóa hoàn toàn glucozo tạo ra axit gluconic

(b) Phản ứng thủy phân xenlulozo xảy ra được trong dạ dày của động vật ăn cỏ.

(c) Xenlulozo trinitrat là nguyên liệu để sản xuất tơ nhân tạo.

(d) Saccarozo bị hóa đen trong H2SO4 đặc.

(e) Trong công nghiệp dược phẩm, saccarozo được dung để pha chế thuốc.

Trong các phát biểu trên, số phát biểu đúng là

Cho hàm số $y=f\left( x \right) $có đồ thị như hình vẽ bên.

Mệnh đề nào sau đây đúng về hàm số đó ?

Cho hàm số $y=f\left( x \right)$ liên tục trên $\left[ a\,;\,b \right]$ và có ${f}'\left( x \right)>0\,\forall x\in \left[ a\,;\,b \right]$, khẳng định nào sau đây sai?

Bảng biến thiên trong hình dưới là của hàm số nào trong các hàm số đã cho ?

Tích của giá trị nhỏ nhất và giá trị lớn nhất của hàm số $f\left( x \right)=x+\frac{x}{4}$ trên đoạn $\left[ 1;3 \right]$ bằng:

Tìm tọa độ giao điểm $I$ của đồ thị hàm số \[y=4{{x}^{3}}-3x\] với đường thẳng \[y=-x+2\].

Trong không gian với hệ tọa độ Oxyz có bao nhiêu mặt phẳng song song với mặt phẳng $\left( Q \right):x+y+z+3=0,$ cách điểm $M\left( 3;2;1 \right)$ một khoảng bằng $3\sqrt{3}$ biết rằng tồn tại một điểm$ X\left( a;b;c \right)$ trên mặt phẳng đó thỏa mãn

$a+b+c<-2?$

Trong các hàm số sau đây, hàm số nào không có cực trị.

Cho hàm số  $y=f\left( x \right)$ có bảng biến thiên:

Hỏi hàm số đó là hàm số nào ?

Hàm số \[y=\frac{mx+1}{x+m}\] đồng biến trên khoảng 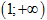 khi:

Giá trị nhỏ nhất của hàm số $y=1+x+\frac{4}{x}$ trên đoạn $\left[ -3;-1 \right]$ bằng:

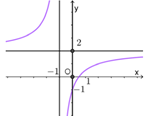
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án \[A,\text{ }B,\text{ }C,\text{ }D\] dưới đây. Hỏi hàm số đó là hàm số nào?

Cho mặt phẳng 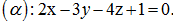  Khi đó, một véc- tơ pháp tuyến của

Phương trình tiếp tuyến của đồ thị hàm số $y=2{{x}^{3}}+5\text{x}+1$ tại điểm có tung độ bằng 1 là:

Cho hàm số \[f\left( x \right)\] đồng biến trên tập số thực \[\mathbb{R}\], mệnh đề nào sau đây là đúng ?

Đường cong trong hình bên dưới là đồ thị của một hàm số trong bốn hàm số dược liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

Cho các este: CH3COOC6H5 (1); CH3COOCH=CH2(2); CH2=CHCOOCH=CHCH3 (3); HCOOCH2CH=CH2 (4); CH3COOCH2C6H5 (5). Những este khi thủy phân trong môi trường kiềm không tạo ra ancol là:

Đồ thị hàm số $y=-{{x}^{4}}+{{x}^{2}}$ có số giao điểm với trục Ox là:

Hàm số $f\left( x \right)$ có đạo hàm $f'\left( x \right)$ trên khoảng $\text{K}$. Hình vẽ bên là đồ thị của hàm số $f'\left( x \right)$ trên khoảng $\text{K}$. Số điểm cực trị của hàm số đã cho là

Cho đường cong $\left( C \right)$ có phương trình $y=\frac{x-1}{x+1}$. Gọi $M$ là giao điểm của  $\left( C \right)$ với trục tung. Tiếp tuyến của $\left( C \right)$ tại $M$ có phương trình là

Gọi \[S\]là tập hợp tất cả các giá trị nguyên dương của tham số thực \[m\]sao cho hàm số $y=\frac{{{x}^{4}}}{4}-\frac{3}{2}m{{x}^{2}}+2x+\frac{2}{{{x}^{2}}}$ đồng biến trên nửa khoảng 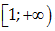. Số phần tử của tập \[S\] là

Cho hàm số $y=-2{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ  thị  như hình dưới. Khẳng định nào sau đây đúng ?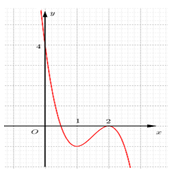 

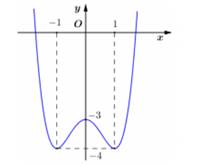
Cho đồ thị hàm số $y=f\left( x \right)$ như hình vẽ.  Đồ thị hàm số $y=f\left( \left| x-2 \right| \right)+1$ có mấy cực trị?

Cho các số thực $x,y$ thỏa mãn $x+y+1=2\left( \sqrt{x-2}+\sqrt{y+3} \right).$ Giá trị lớn nhất của $x+y$.

Xét các khẳng định sau:

(I). Nếu hàm số $y=f\left( x \right)$ có giá trị cực đại là M và giá trị cực tiểu là m thì$M>m$

(II). Đồ thị hàm số $y=a\,{{x}^{4}}+b{{x}^{2}}+c\left( a\ne 0 \right)$ luôn có ít nhất một điểm cực trị.

(III). Tiếp tuyến (nếu có) tại một điểm cực trị của đồ thị hàm số luôn song song với trục hoành.

Số khẳng định đúng là :

Cho hàm số\[y={{x}^{3}}-3m{{x}^{2}}+6,\]. Tìm m để giá trị nhỏ nhất của hàm số trên \[\left[ 0;3 \right]\] bằng 2.

Tìm các giá trị của tham số m để phương trình ${{x}^{2}}\left| {{x}^{2}}-2 \right|=m$ có đúng 4 nghiệm thực phân biệt là:

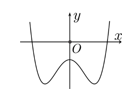
Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng?  

Cho hàm số $y=f(x)=x+\sqrt{1-{{x}^{2}}}$.Tìm tất cả các giá thực của tham số $m$thỏa mãn$f(x)\le m$ với mọi $x\in \text{ }\!\![\!\!\text{ }-\text{1;1 }\!\!]\!\!\text{ }$.

Cho hàm số $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ

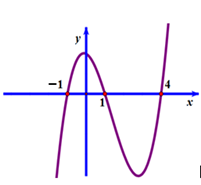Hàm số $y=f\left( 3-2x \right)+2018$ nghịch biến trên khoảng

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$  và có đồ thị của hàm $y=f'\left( x \right)$ như hình vẽ.

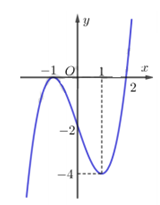
Xét hàm số $g\left( x \right)=f\left( 2-{{x}^{2}} \right).$ Mệnh đề nào dưới đây sai ?

Biết rằng hai đường tiệm cận của đồ thị hàm số $y=\frac{2x+1}{x-m}$ (với m là tham số) tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 2. Tìm tất cả giá trị của m.

Cho hàm số bậc ba $y=f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có $a>0$  và đồ thị hàm số $y=|f(x)|$ như hình vẽ ở bên. Tìm tập hợp tất cả các giá trị m để phương trình \[f(|x|)=m\] có đúng 4 nghiệm thực phân biệt.

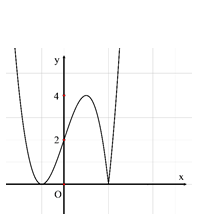
Cho hàm số $f\left( x \right)=\left| 8{{\text{x}}^{4}}+a{{x}^{2}}+b \right|,$ trong đó a, b là các tham số thực. Biết rằng giá trị lớn nhất của hàm số $f\left( x \right)$ trên đoạn \[[-1;1]\] bằng 1. Hãy chọn khẳng định đúng.

Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên như hình vẽ:

Đồ thị hàm số \[y=\left| f\left( x \right)-2m \right|\] có 5 điểm cực trị khi và chỉ khi:

Cho hàm số $y=f\left( x \right)$ xác định và liên tục trên $\mathbb{R}$, có bảng biến thiên như sau

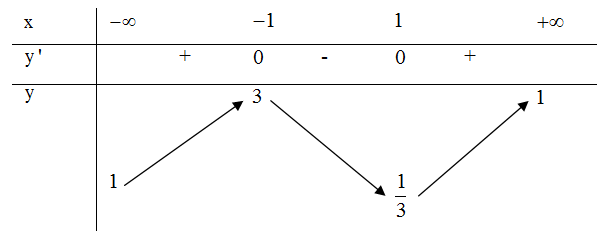
Số nghiệm của phương trình $2{{\left[ f\left( x \right) \right]}^{2}}-3f\left( x \right)+1=0$ là

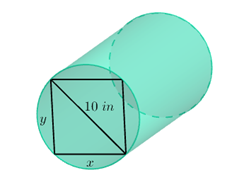
Trong lĩnh vực xây dựng, độ bền d của một thành xà bằng gỗ có dạng một khối trụ (được cắt từ một khúc gỗ, với các kích thước như hình bên dưới; biết 1 in bằng 2,54cm) được tính theo công thức $d=13,8x{{y}^{2}}.$ Giá trị gần đúng của x sao cho thanh xà có độ bền cao nhất là

Cho hàm số \[y=f\left( x \right)\] có đạo hàm liên tục trên đoạn \[\left[ 0;\frac{\pi }{4} \right]\] và \[f\left( \frac{\pi }{4} \right)=0\]. Biết \[\int\limits_{0}^{\frac{\pi }{4}}{{{f}^{2}}\left( x \right)dx=\frac{\pi }{8}},\,\,\int\limits_{0}^{\frac{\pi }{4}}{f'\left( x \right)\sin 2xdx=-\frac{\pi }{4}}\]. Tính tích phân \[I=\int\limits_{0}^{\frac{\pi }{8}}{f\left( 2x \right)dx}\].