đề lafan jnfodnfoidnfoinfinwnveow

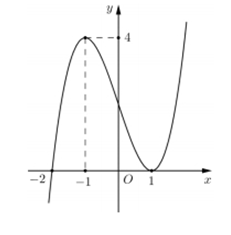
Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}.$ Đường cong trong hình vẽ bên là đồ thị của hàm số $y=f'\left( x \right).$ Xét hàm số $g\left( x \right)=f\left( {{x}^{2}}-3 \right).$ Mệnh đề nào dưới đây sai ? 

Tìm tất cả các giá trị của tham số m để hàm số $f\left( x \right)=\left( {{m}^{2}}-4 \right){{x}^{3}}+3\left( m-2 \right){{x}^{2}}+3x-4$ đồng biến trên $\mathbb{R}.$

Gọi $M\left( a;\,b \right)$ là điểm trên đồ thị hàm số $y\,\,=\,\,\,\frac{x-2}{x}$ sao cho khoảng cách từ $M$ đến đường thẳng $d\,\,:\,\,y=2x\,\,+\,\,6$ nhỏ nhất. Tính ${{\left( 4a\,\,+\,\,5 \right)}^{2}}+{{\left( 2b\,\,-\,\,7 \right)}^{2}}.$

Hình bên là đồ thị của ba hàm số $y={{a}^{x}},y={{b}^{x}},y={{c}^{x}}\left( 0

Tìm giá trị lớn nhất của hàm số $f\left( x \right)=2{{x}^{3}}+3{{x}^{2}}-12x+2$ trên đoạn $\left[ -1;2 \right]$.

Một đoàn cứu trợ lũ lụt đang ở vị trí A của một tỉnh miền trung muốn đên xã C để tiếp tế lương thực và thuốc men, phải đi theo con đường từ A đến B và từ B đến C (như hình vẽ)

Tuy nhiên, do nước ngập con đường từ A đến B nên đoàn cứu trợ không thể đên C bằng xe, nhưng đoàn cứu trợ có thể chèo thuyền từ A đến D với vận tốc ${4km}/{h}\;,$ rồi đi bộ đên C với vận tốc ${6km}/{h}\;.$.Biết A cách B một khoảng $5km,$ B cách C một khoảng $7km.$ Hỏi vị trí D cách A bao xa để đoàn cứu trợ đi đến C nhanh nhất?Một đoàn cứu trợ lũ lụt đang ở vị trí A của một tỉnh miền trung muốn đên xã C để tiếp tế lương thực và thuốc men, phải đi theo con đường từ A đến B và từ B đến C (như hình vẽ).Tuy nhiên, do nước ngập con đường từ A đến B nên đoàn cứu trợ không thể đên C bằng xe, nhưng đoàn cứu trợ có thể chèo thuyền từ A đến D với vận tốc ${4km}/{h}\;,$ rồi đi bộ đên C với vận tốc ${6km}/{h}\;.$.Biết A cách B một khoảng $5km,$ B cách C một khoảng $7km.$ Hỏi vị trí D cách A bao xa để đoàn cứu trợ đi đến C nhanh nhất?

Gọi $m$ và $M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số $f\left( x \right)={{e}^{2-3x}}$ trên đoạn $\left[ 0;2 \right]$. Mối liên hệ giữa $m$ và $M$ là:

Cho một tấm bìa hình chữ nhật có chiều dài $AB=60$cm và chiều rộng $BC=40$cm. Người ta cắt 6 hình vuông, mỗi hình vuông có cạnh bằng $x$ cm, rồi gập tấm bìa lại để được một cái hộp có nắp đậy (tham khảo hình vẽ bên dưới). Giá trị của $x$ sao cho thể tích của khối hộp lớn nhất là

Cho hàm số $y={{x}^{4}}-2m{{x}^{2}}+2m.$ Xác định tất cả các giá trị của m để đồ thị hàm số có ba điểm cực trị và các điểm cực trị này lập thành một tam giác có diện tích bằng 32.

Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ -2;2 \right],$ và có đồ thị là đường cong như trong hình vẽ bên.

Hỏi phương trình $\left| f\left( x \right)-1 \right|=1$ có bao nhiêu nghiệm phân biệt trên đoạn $\left[ -2;2 \right]$.

Cho đồ thị hàm số $y=f\left( x \right)$ như hình vẽ.  Đồ thị hàm số $y=f\left( \left| x-2 \right| \right)+1$ có mấy cực trị?

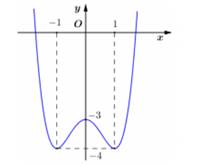
Cho hàm số $y=f\left( x \right).$ Hàm số$y'=f'\left( x \right)$có đồ thị như hình bên. Hàm số $y=f\left( {{x}^{2}} \right)$ đồng biến trên khoảng

Cho hàm số $y=f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ là $f'\left( x \right)=\left( 2x+1 \right)\left( x-3 \right){{\left( x+5 \right)}^{4}}$. Hàm số đã cho có tất cả bao nhiêu điểm cực trị?

Cho hàm số $y=\frac{x+1}{x-2}$. Số các giá trị tham số m để đường thẳng $y=m+x$ luôn cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho trọng tâm tam giác OAB nằm trên đường tròn ${{x}^{2}}+{{y}^{2}}-3y=4$ là:

Cho hàm số $y=f\left( x \right)$ có $f'\left( x \right)=\frac{1}{x+1}$ . Biết rằng $f\left( 0 \right)=2018$. Giá trị của biểu thức $f\left( 3 \right)-f\left( 1 \right)$ bằng:

Tìm tất cả các giá trị của m để đường thẳng \[y=m\] cắt đồ thị hàm số \[y=2{{\left| x \right|}^{3}}-9{{x}^{2}}+12\left| x \right|\] tại 6 điểm phân biệt

Cho hàm số \[y=f\left( x \right)\] đạo hàm $f'\left( x \right)=-{{x}^{2}}-1.$ Với các số thực dương a, b thỏa mãn $a

Tìm tất cả các giá trị của tham số m để đồ thị hàm số  $y={{x}^{4}}-2m{{x}^{2}}+2m+{{m}^{4}}$ có 3 điểm cực trị tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 2 lần bán kính đường tròn nội tiếp ?

Cho hàm số \[\text{y}=\text{f}\left( \text{x} \right)\] xác định, liên tục trên $\mathbb{R}$và có bảng biến thiên :

Phương trình \[2.\text{f}\left( \text{x} \right)-3=0\] có bao nhiêu nghiệm ?

Cho đồ thị hàm số $y=f\left( x \right)=-{{x}^{3}}+3x-2$ như hình vẽ.

Phương trình $\left| x+2 \right|{{\left( x-1 \right)}^{2}}=m$ có đúng $2$ nghiệm phân biệt khi và chỉ khi:

Gọi A là tập hợp các giá trị của tham số m sao cho hàm số $y={{x}^{3}}-3{{x}^{2}}+\left( {{m}^{2}}-2m \right)x-1$ có hai điểm cực trị ${{x}_{1}},\,{{x}_{2}}$ thỏa \[x_{1}^{2}+x_{2}^{2}=2.\] Số phần tử của tập hợp A là

 

Cho hàm số $y=f\left( x \right)$. Đồ thị của hàm số $y={{f}^{'}}\left( x \right)$ như hình bên. Đặt $h\left( x \right)=f\left( x \right)-\frac{{{x}^{2}}}{2}$. Mệnh đề nào dưới đây đúng ?

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x)=-2x^{4}+4x^{2}+3$ trên đoạn [0; 2] lần lượt là:

Tất cả các giá trị của $m$ để phương trình $mx-\sqrt{x-3}=m+1$ có hai nghiệm thực phân biệt.

Cho hàm số . Tồn tại hai tiếp tuyến của $\left( C \right)$ phân biệt và có cùng hệ số góc k, đồng thời đường thẳng đi qua các tiếp điểm của hai tiếp tuyến đó cắt các trục Ox, Oy tương ứng tại A và B sao cho $OA=2017.$ Hỏi có bao nhiêu giá trị của k thỏa mãn yêu cầu bài toán ?

Tìm tất cả các giá trị của tham số $m$ để bất phương trình $\left( 3m+1 \right){{12}^{x}}+\left( 2-m \right){{6}^{x}}+{{3}^{x}}\le 0$ có nghiệm đúng với $\forall x>0$.

Giả sử hàm số \[y=\frac{{{x}^{2}}+3x+m-1}{x-3}\] đạt cực trị tại các điểm \[{{x}_{1}},{{x}_{2}}\]. Tính \[\left| \frac{y\left( {{x}_{1}} \right)-y\left( {{x}_{2}} \right)}{{{x}_{1}}-{{x}_{2}}} \right|\].

 Cho hàm số $y={{x}^{3}}+3m{{x}^{2}}+\left( m+1 \right)x+1$ có đồ thị \[\left( C \right).\] Với giá trị nào của tham số $m$ thì tiếp tuyến với đồ thị \[\left( C \right)\] tại điểm có hoành độ bằng \[-1\] đi qua \[A\left( 1;3 \right)\]?

Tìm tất cả các giá trị của m để hàm số \[y={{x}^{3}}-3m{{x}^{2}}+3(2m-1)x+7\] nghịch biến trên khoảng có độ dài bằng hai ?

Với giá trị nào của m thì hàm số \[y=\frac{\left( m+1 \right)x+2m+2}{x+m}\] nghịch biến trong khoảng \[\left( -1;+\infty\right)\].