Đề luyện thi đại học2019

 Số nghiệm của phương trình $\frac{{{x}^{2}}}{2}+x-\ln \left( {{x}^{2}}-2 \right)=2018$ là:

Cho hàm số \[f(x)={{\ln }^{2}}({{x}^{2}}-2x+4)\]. Tìm các giá trị của x để \[f'(x)>0.\]

Cho tam giác ABC với \[A\left( 2;-3;2 \right),\text{ B}\left( 1;-2;2 \right),\text{ C}\left( 1;-3;3 \right).\] Gọi A’, B’, C’ lần lượt là hình chiếu vuông góc của A, B, C lên mặt phẳng 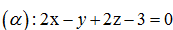Khi đó, diện tích tam giác A’B’C’ bằng:

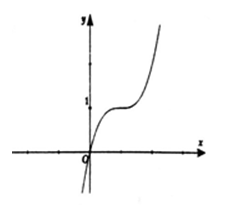
 Cho hàm số bậc 3 \[y=a{{x}^{3}}+b{{x}^{2}}+cx+d\] có đồ thị như hình vẽ.

Giá trị nhỏ nhất của biểu thức \[P={{a}^{2}}+{{c}^{2}}+b+1\] là :

Hãy lập phương trình đường thẳng (d) đi qua các điểm cực đại và cực tiểu của đồ thị hàm số \[y={{x}^{3}}+3m{{x}^{2}}-3x\].