Đề thi hàm số

Cho hàm số $y=f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ là $f'\left( x \right)=\left( 2x+1 \right)\left( x-3 \right){{\left( x+5 \right)}^{4}}$. Hàm số đã cho có tất cả bao nhiêu điểm cực trị?

Tìm tất cả các giá trị của tham số m để đồ thị hàm số \[y={{x}^{3}}+2{{x}^{2}}+\left( m-3 \right)x+m\] có 2 điểm cực trị và điểm \[M\left( 9;-5 \right)\] nằm trên đường thẳng đi qua hai điểm cực trị của đồ thị hàm số. 

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=\frac{1}{3}{{x}^{3}}-\frac{1}{2}m{{x}^{2}}+2mx-3m+4$ nghịch biến trên đoạn có độ dài là 3?

Có bao nhiêu giá trị nguyên của tham số thực $m$để hàm số $y=\frac{2x-m}{x+1}$ đồng biến trên mỗi khoảng $(-\infty \,;\,-1)$và $(-1\,;\,\,+\infty )$ và hàm số $y=\frac{-2x-m}{x+2}$ nghịch biến trên mỗi khoảng $(-\infty \,;\,-2)$và $(-2\,;\,+\infty )$?

Hàm số nào dưới đây có đồ thị như hình vẽ

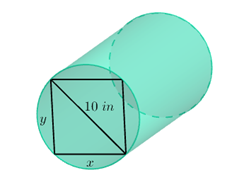
Trong lĩnh vực xây dựng, độ bền d của một thành xà bằng gỗ có dạng một khối trụ (được cắt từ một khúc gỗ, với các kích thước như hình bên dưới; biết 1 in bằng 2,54cm) được tính theo công thức $d=13,8x{{y}^{2}}.$ Giá trị gần đúng của x sao cho thanh xà có độ bền cao nhất là

Tìm giá trị lớn nhất của hàm số $f\left( x \right)=2{{x}^{3}}+3{{x}^{2}}-12x+2$ trên đoạn $\left[ -1;2 \right]$.

Cho hàm số có đồ thị (C): $y=\frac{2x+1}{x-1}$. Gọi M là điểm bất kì thuộc đồ thị (C). Gọi tiếp tuyến của đồ thị (C) tại M cắt các tiệm cận của (C) tại hai điểm P và Q. Gọi G là trọng tâm tam giác IPQ (với I là giao điểm của hai đường tiệm cận của (C)). Diện tích tam giác GPQ là

Cho hàm số 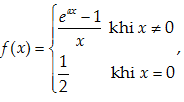 với \[a\ne 0\]. Tìm giá trị của a để hàm số \[f(x)\] liên tục tại \[{{x}_{0}}=0.\]

Cho hàm số $y=f\left( x \right)$ liên tục trên có bảng biến thiên như sau: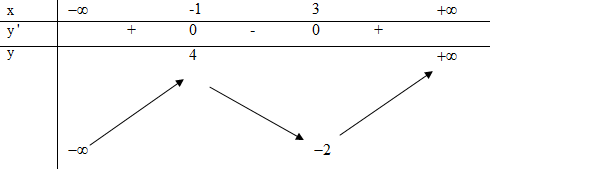

Biết $f\left( 0 \right)

Tìm tất cả các giá trị của tham số m sao cho phương trình ${{x}^{3}}-3{{x}^{2}}+\left( 2m-2 \right)x+m-3=0$ có ba nghiệm ${{x}_{1}};{{x}_{2}};{{x}_{3}}$ thỏa mãn ${{x}_{1}}

Cho hàm số bậc ba $y=f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có $a>0$  và đồ thị hàm số $y=|f(x)|$ như hình vẽ ở bên. Tìm tập hợp tất cả các giá trị m để phương trình \[f(|x|)=m\] có đúng 4 nghiệm thực phân biệt.

Cho hàm số $f\left( x \right)$ có đạo hàm lad $f'\left( x \right).$ Đồ thị hàm số $y=f'\left( x \right)$ được cho như hình bên. Biết rằng $f\left( 0 \right)+f\left( 3 \right)=f\left( 2 \right)+f\left( 5 \right).$ Gía trị nhỏ nhất, giá trị lớn nhất của $f\left( x \right)$ trên đoạn $\left[ 0;5 \right]$ lần lượt là

Tập hợp các giá trị của $m$ để đồ thị của hàm số $y=\frac{2x-1}{\left( m{{x}^{2}}-2x+1 \right)\left( 4{{x}^{2}}+4m+1 \right)}$ có đúng $1$ đường tiệm cận là:

Cho một tấm bìa hình chữ nhật có chiều dài $AB=60$cm và chiều rộng $BC=40$cm. Người ta cắt 6 hình vuông, mỗi hình vuông có cạnh bằng $x$ cm, rồi gập tấm bìa lại để được một cái hộp có nắp đậy (tham khảo hình vẽ bên dưới). Giá trị của $x$ sao cho thể tích của khối hộp lớn nhất là

Gọi \[S=\left( -\infty ;\frac{a}{b} \right]\] (với \[\frac{a}{b}\] là phân số tối giản, \[a\in Z,b\in {{N}^{*}}\]) là tập hợp tất cả các giá trị của tham số m sao cho phương trình \[\sqrt{2{{x}^{2}}+mx+1}=x+3\] có hai nghiệm phân biệt. Tính \[B={{a}^{2}}-{{b}^{3}}.\]

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:

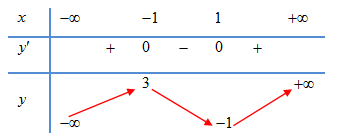
Tìm số nghiệm của phương trình $2\left| f\left( x \right) \right|-1=0$. 

Có bao nhiêu giá trị nguyên của tham số m để phương trình $m{{\left( {{x}^{2}}+2x \right)}^{3}}-2{{x}^{2}}-4x+2=0$ có nghiệm thỏa mãn \[x\le -3?\]

Tìm tất cả các giá trị của m để đường thẳng \[y=m\] cắt đồ thị hàm số \[y=2{{\left| x \right|}^{3}}-9{{x}^{2}}+12\left| x \right|\] tại 6 điểm phân biệt

Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y=\sqrt{1-{{x}^{2}}}+2\sqrt[3]{{{\left( 1-{{x}^{2}} \right)}^{2}}}.\] Hỏi điểm \[A\left( M;m \right)\] thuộc đường tròn nào sau đây ?

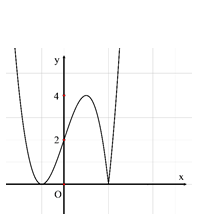
Cho hàm số \[y={{x}^{4}}-4{{x}^{2}}+3\] có đồ thị như hình vẽ. Tìm số cực trị của hàm số \[y=\left| {{x}^{4}}-4{{x}^{2}}+3 \right|\].

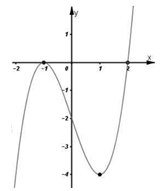
Cho hàm số \[f\left( x \right)\] có đạo hàm trên \[R\] và có đồ thị hàm \[y=\text{ }f'\left( x \right)\] như hình vẽ. Xét hàm số \[g\left( x \right)=f\left( {{x}^{2}}-2 \right).\] Mệnh đề nào dưới đây sai ?

Cho hàm số \[y=m{{x}^{4}}+\left( {{m}^{2}}-9 \right){{x}^{3}}+10\]. Tìm m để hàm số có 3 điểm cực trị.

Gọi ${{x}_{1}},{{x}_{2}}$ lần lượt là điểm cực đại và cực tiểu của hàm số $y=\frac{{{x}^{2}}-2x+1}{x-2}$. Giá trị của biểu thức $2{{x}_{1}}+3{{x}_{2}}$ bằng

Biết rằng hai đường tiệm cận của đồ thị hàm số $y=\frac{2x+1}{x-m}$ (với m là tham số) tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 2. Tìm tất cả giá trị của m.

Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên như hình vẽ:

Đồ thị hàm số \[y=\left| f\left( x \right)-2m \right|\] có 5 điểm cực trị khi và chỉ khi:

Tiếp tuyến của đồ thị hàm số $y=\frac{4x-3}{2x+1}$ cùng với 2 tiệm cận tạo thành  một tam giác có diện tích bằng:

Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn

$\left[ -2017;2017 \right]$ để hàm số $y={{x}^{3}}-6{{x}^{2}}+mx+1$ đồng biến trên khoảng

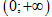
Cho hàm số $y=\frac{2x-1}{x+1}$ có đồ thị $\left( C \right)$. Tìm tất cả các giá trị của tham số $m$ để đường thẳng $d:y=-x+m$ cắt đồ thị $\left( C \right)$ tại hai điểm phân biệt $A$ và $B$ đều có hoành độ âm.

Gọi $m$ và $M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số $f\left( x \right)={{e}^{2-3x}}$ trên đoạn $\left[ 0;2 \right]$. Mối liên hệ giữa $m$ và $M$ là:

Cho hàm số $y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d,\,\,\left( a,b,c,d\in \mathbb{R} \right),$ có bảng biến thiên như hình sau:

Tìm tất cả giá trị thực của tham số $m$ để phương trình $m=\left| f\left( x \right) \right|$ có $4$ nghiệm phân biệt trong đó có đúng một nghiệm dương.

Tính giá trị nhỏ nhất và giá trị lớn nhất của hàm số $f\left( x \right) = x + \frac{4}{x}$ trên $\left[ {1;4} \right]$ bằng

Phương trình \[{{x}^{3}}+x\left( x+1 \right)=m{{\left( {{x}^{2}}+1 \right)}^{2}}\] có nghiệm thực khi và chỉ khi: 

Tìm giá trị m để đường thẳng $\left( d \right):y=\left( 2m+1 \right)x-m+3$ vuông góc với đường thẳng đi hai điểm cực trị của đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}+1$. 

Cho đồ thị $\left( C \right):{{x}^{3}}-3{{x}^{2}}.$ Có bao nhiêu số nguyên $b\in \left( -10;10 \right)$ để có đúng một tiếp tuyến của $\left( C \right)$ đi qua điểm $B\left( 0;b \right)?$

Biết hàm số \[f(x)=\frac{a}{{{b}^{2}}{{.3}^{x}}}\] có đồ thị đối xứng với đồ thị hàm số \[y=\text{ }{{3}^{x}}\] qua đường thẳng x = −1. Biết a,b là các số nguyên.

Chọn khẳng định đúng trong các khẳng định sau:

Cho hàm số \[y=f\left( x \right)\] đạo hàm $f'\left( x \right)=-{{x}^{2}}-1.$ Với các số thực dương a, b thỏa mãn $a

Tìm tập giá trị T của hàm số $y=\sqrt{x-3}+\sqrt{5-x}$. 

Với giá trị nào của m thì hàm số \[y=\frac{\left( m+1 \right)x+2m+2}{x+m}\] nghịch biến trong khoảng \[\left( -1;+\infty\right)\].

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ đồng thời hàm số $y=\left| f\left( x \right) \right|$ có đồ thị như hình vẽ bên.

Xác định số cực trị của hàm số $y=f\left( \left| x \right| \right)$