Đề thi thành phần

Cho các số thực $x,y$ thỏa mãn $x+y+1=2\left( \sqrt{x-2}+\sqrt{y+3} \right).$ Giá trị lớn nhất của $x+y$.

Cho đồ thị $\left( C \right)$ của hàm số $y=\frac{2x+2}{x-1}.$Tọa độ điểm M nằm trên $\left( C \right)$ sao cho tổng khoảng cách từ M đến hai tiệm cận của $\left( C \right)$ nhỏ nhất là:

Cho hàm số \[y=\frac{x+2}{x-2}\] có đồ thị \[\left( C \right)\]. Gọi \[I\] là giao điểm hai đường tiệm cận của \[\left( C \right)\]. Tiếp tuyến của \[\left( C \right)\] cắt hai đường tiệm cận của \[\left( C \right)\] tại hai điểm \[A,B\]. Giá trị nhỏ nhất của chu vi đường tròn ngoại tiếp tam giác \[IAB\] bằng

Cho hàm số \[y={{x}^{3}}-3{{x}^{2}}-\left( {{m}^{2}}-2 \right)x+{{m}^{2}}\] có đồ thị là đường cong \[\left( C \right)\]. Biết rằng các số thực \[{{m}_{1}};\,\,{{m}_{2}}\] của tham số m để hai điểm cực trị của \[\left( C \right)\] và giao điểm của \[\left( C \right)\] với trục hoành tạo thành 4 đỉnh của hình chữ nhật. Tính \[T=m_{1}^{4}+m_{2}^{4}\].

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$  và có đồ thị của hàm $y=f'\left( x \right)$ như hình vẽ.

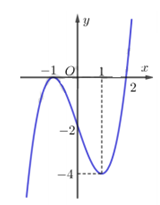
Xét hàm số $g\left( x \right)=f\left( 2-{{x}^{2}} \right).$ Mệnh đề nào dưới đây sai ?

Gọi $M,\text{ }N$lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y={{x}^{2}}.{{e}^{-x}}$trên đoạn $\left[ -1;1 \right]$. Tính tổng $M+N$.

Gọi S là tổng tất cả các giá trị của tham số m để hàm số $y={{x}^{3}}+\left( {{m}^{2}}+1 \right)x-m+1$ có giá trị lớn nhất trên đoạn $\left[ 0;1 \right]$ bằng 9. Giá trị của S bằng:

Tìm điều kiện của m để đồ thị hàm số $y=\frac{x}{\sqrt{1-m{{x}^{2}}}}$ có hai tiệm cận ngang.

Với giá trị thực nào của tham số m th̀ì đường thẳng $y=2x+m$ cắt đồ thị của hàm số $y=\frac{x+3}{x+1}$  tại hai điểm phân biệt M, N sao cho MN ngắn nhất?

Tìm tất cả các giá trị của tham số m để đồ thị hàm số \[y={{x}^{3}}+2{{x}^{2}}+\left( m-3 \right)x+m\] có 2 điểm cực trị và điểm \[M\left( 9;-5 \right)\] nằm trên đường thẳng đi qua hai điểm cực trị của đồ thị hàm số. 

Tìm giá trị thực của tham số m đê hàm số $y=\frac{1}{3}{{x}^{3}}-m{{x}^{2}}+\left( {{m}^{2}}-4 \right)x+3$ đạt cực đại tại $x=3$.

Hàm số \[y=\frac{2\sin 2x+\cos 2x}{\sin 2x-\cos 2x+3}\] có tất cả bao nhiêu giá trị nguyên?

Có bao nhiêu giá trị nguyên của \[m\] để hàm số \[f\left( x \right)={{x}^{3}}+3{{x}^{2}}-\left( {{m}^{2}}-3m+2 \right)x+5\] đồng biến trên \[\left( \text{ }0;2\text{ } \right)\text{ }?\] 

Cho hàm số . Tồn tại hai tiếp tuyến của $\left( C \right)$ phân biệt và có cùng hệ số góc k, đồng thời đường thẳng đi qua các tiếp điểm của hai tiếp tuyến đó cắt các trục Ox, Oy tương ứng tại A và B sao cho $OA=2017.$ Hỏi có bao nhiêu giá trị của k thỏa mãn yêu cầu bài toán ?

Có bao nhiêu giá trị của tham số $m$ để phương trình trình \[{{4}^{x}}-{{2.2}^{x}}+2=m\] có nghiệm \[x\in \left( -1;2 \right)\].

Số giá trị nguyên dương của tham số m để hàm số $y={{\left( \frac{1}{2} \right)}^{{{x}^{3}}-6{{\text{x}}^{2}}+m\text{x}+2}}$ luôn đồng biến trên khoảng $\left( 1;3 \right)$ là:

Tìm tất cả các giá trị của tham số m sao cho phương trình ${{x}^{3}}-3{{x}^{2}}+\left( 2m-2 \right)x+m-3=0$ có ba nghiệm ${{x}_{1}};{{x}_{2}};{{x}_{3}}$ thỏa mãn ${{x}_{1}}

Có bao nhiêu giá trị nguyên của tham số m để đường thẳng $y=m\left( x-4 \right)$ cắt đồ thị của hàm số $y=\left( {{x}^{2}}-1 \right)\left( {{x}^{2}}-9 \right)$ tại bốn điểm phân biệt ?

Phương trình \[{{x}^{3}}+x\left( x+1 \right)=m{{\left( {{x}^{2}}+1 \right)}^{2}}\] có nghiệm thực khi và chỉ khi: 

Cho hàm số $y=x\left( {{x}^{2}}-3 \right)$ có đồ thị $\left( C \right)$. Có bao nhiêu điểm M thuộc đồ thị $\left( C \right)$ thỏa mãn tiếp tuyến tại M của $\left( C \right)$cắt $\left( C \right)$và trục hoành lần lượt tại hai điểm phân biệt A (khác M) và B sao cho M là trung điểm của đoạn thẳng AB?

Cho hàm số \[y=f(x)\] có bảng biến thiên như sau:Đồ thị hàm số \[y=\frac{1}{f(3-x)-2}\] có bao nhiêu tiệm cận đứng.

: Cho hàm số $y=\frac{x+m}{x+1}$ (m là tham số thực) thỏa mãn\[\underset{\left[ 0;1 \right]}{\mathop{\min }}\,\,y=3.\] Mệnh đề nào dưới đây đúng ?

Cho hàm số $y=\frac{x+1}{x-1}$ có đồ thị $\left( C \right).$ Gọi $A{{x}_{B}}\ge 0 \right)$ là hai điểm trên $\left( C \right)$ có tiếp tuyến tại A,B song song nhau và $AB=2\sqrt{5}.$ Hiệu ${{x}_{A}}-{{x}_{B}}$ bằng ?

Cho $\left( {{C}_{m}} \right):2{{\text{x}}^{3}}-\left( 3m+3 \right){{x}^{2}}+6m\text{x}-4.$ Gọi T là tập hợp các giá trị của m thỏa mãn $\left( {{C}_{m}} \right)$ có đúng hai điểm chung với trục hoành, tính tổng S các phần tử của T.

Cho hàm số \[y=\frac{\left( m+2 \right)}{3}{{x}^{3}}-(m+2){{x}^{2}}-(3m-1)x+3\]. Tìm m để hàm số đồng biến trên khoảng (-∞;+∞).