đẹp trai ko thể sai

Cho hàm số $y=\frac{x-1}{2x-3}.$ Gọi I là giao điểm của hai tiệm cận của đồ thị hàm số. Khoảng cách từ I đến tiếp tuyến của đồ thị hàm số đã cho đạt giá trị lớn nhất bằng:

Tính giá trị nhỏ nhất và giá trị lớn nhất của hàm số $f\left( x \right) = x + \frac{4}{x}$ trên $\left[ {1;4} \right]$ bằng

Cho hàm số $y=\frac{{{2}^{x+1}}+1}{{{2}^{x}}-m}$ với m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m trong khoảng $\left( -50;50 \right)$ để hàm số ngịch biến trên $\left( -1;1 \right).$ Số phần tử của S là:

Cho hàm số \[y=f\left( x \right)\] có đạo hàm \[f'\left( x \right)\] trên khoảng.  Đồ thị của hàm số \[y=f\left( x \right)\] như hình vẽ.

Đồ thị của hàm số $y={{\left( f\left( x \right) \right)}^{2}}$ có bao nhiêu điểm cực đại, điểm cực tiểu ?

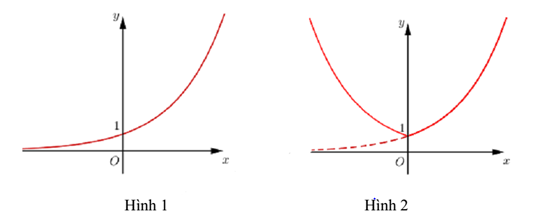
Cho hàm số$y={{\left( \sqrt{2} \right)}^{x}}$có đồ thị là hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

Hỏi có bao nhiêu giá trị m nguyên trong đoạn \[\left[ -2017;2017 \right]\] để hàm số \[y={{x}^{3}}-3\left( 2m+1 \right){{x}^{2}}+\left( 12m+5 \right)x-2\] đồng biến trên khoảng ?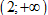 

Tiếp tuyến với đồ thị \[\left( C \right):y={{x}^{3}}-3{{x}^{2}}-2\] song song với đường thẳng \[\left( d \right):y=9x+3\] có phương trình là:

 Cho hàm số $y=f\left( x \right)$ có đồ thị $y=f'\left( x \right)$ cắt trục Ox tại ba điểm có hoành độ $a

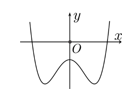
Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ bên dưới. Mệnh đề nào sau đây đúng?  

Tìm tất cả các giá trị của tham số m để phương trình ${{\left| x \right|}^{3}}-3\left| x \right|=2m$ có 4 nghiệm phân biệt.