giữa học kì 1

Số đường tiệm cận đứng của đồ thị hàm số \[y=\frac{{{x}^{2}}-3x+2}{{{x}^{2}}-4}\] là: 

Khi một sóng âm truyền từ nước ra không khí thì

Khẳng định nào sau đây đúng?

Cho hàm số $y=f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

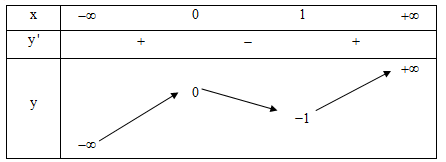
Tìm tất cả các giá trị thực của tham số m để phương trình $f\left( \left| x \right| \right)-2m+1$ có bốn nghiệm phân biệt ?

Tìm số tiêm cân đứng và ngang của đồ thi hàm số $y=\frac{x+1}{{{x}^{3}}-3x-2}.$

Đường cong hình bên dưới là đồ thị của một trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào ?

Một sóng cơ học phát ra từ một nguồn O lan truyền trên mặt nước với bước sóng λ= 30cm. Gọi M, N là hai điểm trên cùng một phương truyền sóng cách O lần lượt 10 cm và 15 cm. So với dao động tại N thì dao động tại M

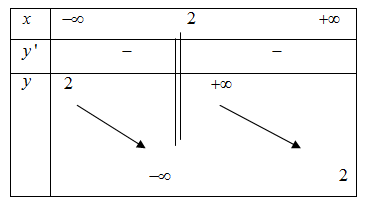
Hàm số nào sau đây có bảng biến thiên như hình vẽ ?

Tìm giá trị nhỏ nhất của hàm số $y=2c\text{os}\frac{x}{2}+\operatorname{s}\text{inx}+1.$

Hàm số \[y=x+\frac{4}{x}\]đồng biến trên khoảng nào ?

Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ bên dưới:

Khẳng định nào sau đây đúng ?

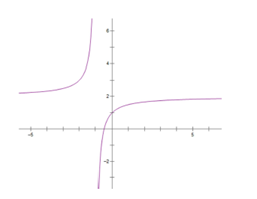
Đồ thị sau đây là của hàm số nào? Chọn 1 câu đúng.

Cho hàm số $y=a{{x}^{3}}+b{{x}^{2}}+3x-2$. Tìm các giá trị của a và b biết hàm số đạt cực trị tại $x=3$ và $y\left( 3 \right)=-2$. 

Đun nóng 5,18 gam mety axetat với 100ml dung dịch NaOH 1M đến phản ứng hoàn toàn. Cô cạn dung dịch sau phản ứng, thu đuợc m gam chất rắn khan. Giá trị của m là:

Hàm số nào sau đây đồng biến trên $\mathbb{R}$. 

Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\frac{1-2x}{-x+2}$ là:

Hàm số \[y=\frac{{{x}^{3}}}{3}-\frac{3}{2}{{x}^{2}}+1\] nghịch biến trên khoảng nào ?

Biết đồ thị hàm số \[y={{x}^{4}}-\left( m-1 \right){{x}^{2}}+{{m}^{2}}-m-1\] cắt trục hoành tại đúng ba điểm phân biệt. Khi đó giá trị của tham số m thuộc khoảng :

Hàm số \[y=\sin x\]đồng biến trên khoảng nào sau đây? 

Trong các hàm số sau, hàm số nào nghịch biến trên khoảng \[\left( 0;\sqrt{2} \right)\] ?