hàm số khó 12

Cho \[x,\text{ }y\] thỏa mãn $\sqrt{2x+3}+\sqrt{y+3}=4.$ Tìm giá trị nhỏ nhất của $P=\sqrt{x+2}+\sqrt{y+9}$.

Cho hàm số $f\left( x \right)$có đạo hàm trên $\mathbb{R}$và có đồ thị hàm $y=f'\left( x \right)$ như hình vẽ. Xét hàm số $g\left( x \right)=f\left( {{x}^{2}}-2 \right)$. Mệnh đề nào dưới đây sai?

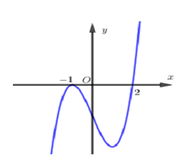
Cho hàm số $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ. Hàm số 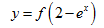đồng biến trên khoảng ?

Hình vẽ bên là đồ thị của hàm số $y=f\left( x \right).$ Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số $y=\left| f\left( x-1 \right)+m \right|$ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:

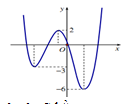
Cho hàm số $y=f\left( x \right)\left( x-1 \right)$liên tục trên $\mathbb{R}$và có đồ thị như hình vẽ.

Tìm tất cả các giá trị của tham số m để phương trình $f\left( x \right)\left| x-1 \right|=m$ có số nghiệm lớn nhất.