kiểm tra chương 1 lớp 12

Cho hàm số $y=f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c$ có bảng biến thiên như hình vẽ dưới đây

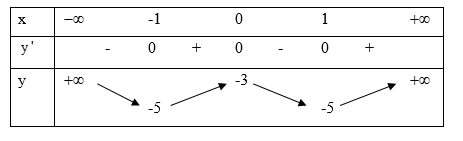
Tính giá trị của biểu thức $P=a+2b+3c$ 

Hàm số nào sau đây đồng biến trên $\mathbb{R}$ ? 

Hỗn hợp X gồm CH3OH, CH2=CH-CH2OH, C3H5(OH)3, C2H4(OH)2. Cho m gam hỗn hợp X tác dụng với Na dư thu được 21,504 lít H2 (đktc). Đốt cháy m gam hỗn hợp X cần 75,712 lít O2 ( đktc) thu được 61,2 gam H2O. Phần trăm khối lượng CH2=CH-CH2OH trong hỗn hợp X là:

Tìm các giá trị của tham số m để hàm số $y=\frac{{{x}^{3}}}{3}-3{{x}^{2}}+{{m}^{2}}x+2m-3$ đồng biến trên$\mathbb{R}$ 

Tìm tọa độ điểm M có hoành độ dương thuộc đồ thị (C) của hàm số $y=\frac{x+2}{x-2}$  sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C) đạt giá trị nhỏ nhất.

Đồ thị hàm số $y=\frac{x-2}{{{x}^{2}}-9}$ có bao nhiêu đường tiệm cận ?

Tìm tất cả các giá trị thực của tham số m để hàm số $y=m\sin x+\frac{1}{3}\sin 3x$ đạt cực đại tại điểm $x=\frac{\pi }{3}$. 

Tìm tất cả giá trị thực của tham số m để hàm số $y={{x}^{3}}-3m{{x}^{2}}+4{{m}^{3}}$ có hai điểm cực trị và B sao cho tam giác OAB có diện tích bằng 4, với O là gốc tọa độ.

Hình bên là đồ thị của hàm số nào ?

Tìm m để hàm số $y={{x}^{3}}-3{{x}^{2}}+mx+2$  tăng trên khoảng .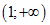 

Thủy phân este E có công thức phân tử C4H8O (có mặt H2SO4 loãng) thu được 2 sản phẩm hữu cơ X và Y. Từ X có thể điều chế trực tiếp ra Y bằng một phản ứng duy nhất. Tên gọi của E là

Hàm số nào sau đây đồng biến trên $\mathbb{R}$. 

Tìm gía trị nhỏ nhất của hàm số\[y=-x+3-\frac{1}{x+2}\] trên nửa khoảng \[\left[ -4;-2 \right)\].

Lên men hoàn toàn a gam glucozo, thu đuợc C2H5OH và CO2. Hấp thụ hết CO2 sinh ra vào dung dịch nuớc vôi trong dư, thu đuợc 15 gam kết tủa. Giá trị của a là:

Xét nguyên tử hiđrô theo mẫu nguyên tử Bo. Khi êlectron chuyển động trên quỹ đạo tròn thì tương đương như một dòng điện tròn. Tỉ số cường độ dòng điện tròn của êlectron khi nguyên tử ở quỹ đạo dừng M và K là

Cho hàm số $y={{x}^{3}}-3{{\text{x}}^{2}}+\left( m+1 \right)x+1$ có đồ thị $\left( {{C}_{m}} \right)$ với m là tham số. Tìm tất cả các giá trị của tham số m để đường thẳng $d:y=x+1$ cắt đồ $\left( {{C}_{m}} \right)$thị tại ba điểm phân biệt $P\left( 0;1 \right),M,N$ sao cho tam giác OMN vuông tại O (O là gốc tọa độ).

Số đồng phân đơn chức ứng với công thức phân tử C4H8O2 là

Chất nào sau đây không thủy phân trong môi trường axit?

Cho hàm số  .  Tìm m để hàm số liên tục tại ${{x}_{0}}=2$

Đồ thị hàm số $y={{x}^{4}}-2{{x}^{2}}+5$ cắt đường thẳng $y=6$ tại bao nhiêu điểm ?