Nguyễn Thị NN

Tập xác định của hàm số \[y=\log \frac{x-{{x}^{2}}}{3-x}\] là:

Cho hàm số $y=f\left( x \right)=\ln \left( \sqrt{1+{{x}^{2}}}+x \right)$. Tập nghiệm của bất phương trình $f\left( a-1 \right)+f\left( \ln a \right)\le 0$ là

Bà Hoa gửi 100 triệu đồng vào tài khoản định kỳ tính lãi kép với lãi suất 8%/năm. Sau 5 năm bà rút toàn bộ tiền và dùng một nửa để sửa nhà, số tiền còn lại bà tiếp tục gửi vào ngân hàng. Tính số tiền lãi thu được sau 10 năm.

Cho số thực dương a, b, c khác 1. Đồ thị các hàm số \[y=\text{ }lo{{g}_{a}}x,\text{ }y=\text{ }lo{{g}_{b}}x,\text{ }y=\text{ }lo{{g}_{c}}x,\text{ }y={{d}^{x}}\] được cho trong hình vẽ bên.

Tìm khẳng định đúng.

Đặt \[a={{\log }_{2}}3;b={{\log }_{3}}5.\]Biểu diễn\[{{\log }_{20}}12\] theo a, b.

Cho phương trình: \[(m~-1)\log _{\frac{1}{2}}^{2}{{\left( x-2 \right)}^{2}}+4\left( m-5 \right){{\log }_{\frac{1}{2}}}\frac{1}{x-2}+4m-4=0\] (với m là tham số). Gọi \[S=~[a;b]\] là tập các giá trị của m để phương trình có nghiệm trên đoạn \[\left[ \frac{5}{2};4 \right]\]. Tính \[a+b.\]

Tìm tập hợp tất cả các tham số m sao cho phương trình ${{4}^{{{x}^{2}}-2x+1}}-m{{.2}^{{{x}^{2}}-2x+2}}+3m-2=0$ có bốn nghiệm phân biệt.

Gọi x, y là các số thực dương thỏa mãn ${{\log }_{9}}x={{\log }_{12}}y={{\log }_{16}}\left( x+y \right)$ và $\frac{x}{y}=\frac{-a+\sqrt{b}}{2},$ với a, b là hai số nguyên dương. Tính \[P=a.b\]

Cho hệ 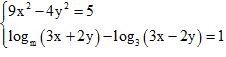 có nghiệm $\left( x;y \right)$ thỏa mãn $3x+2y\le 5.$ Khi đó giá trị lớn nhất của m là:

Cho $a={{10}^{\frac{m}{n-\log b}}};b={{10}^{\frac{m}{n-\log c}}}$ với $a,b,c,m,n$ là các số nguyên sao cho các biểu thức có nghĩa. Tính biểu thức $\log c$ theo $\log a$.