ôn tập toán 12

Cho hai số thực x,y thỏa mãn $0\le x\le \frac{1}{2},\,0

Tìm bộ ba số nguyên dương (a;b;c) thỏa mãn:

log1 + log(1 + 3) + log(1 + 3 + 5) +...+ log(1 + 3 + 5 + ... + 19) − 2log5040 = a + blog2 + clog3

Cho x, y là các số thực thỏa mãn điều kiện ${{3}^{{{x}^{2}}+{{y}^{2}}-2}}.{{\log }_{2}}\left( x-y \right)=\frac{1}{2}\left[ 1+{{\log }_{2}}\left( 1-xy \right) \right].$ Tìm giá trị lớn nhất của biểu thức $M=2\left( {{x}^{3}}+{{y}^{3}} \right)-3xy.$ 

Số  các  giá  trị  nguyên  của  tham  số  m  để  phương  trình ${{\log }_{\sqrt{2}}}\left( x-1 \right)={{\log }_{2}}\left( mx-8 \right)$ có hai nghiệm thực phân biệt là :

Ba anh em Tháng, Mười, Hai cùng vay tiền ở một ngân hàng với lãi xuất 0,7%/tháng với tổng số tiền vay là 1 tỉ đồng. Giả sử mỗi tháng ba người đều trả cho ngân hàng một số tiền như nhau để trừ vào tiền góc và lãi. Để trả hết gốc và lãi cho ngân hàng thì Tháng cần 10 tháng. Mười cần 15 tháng và Hai cần 25 tháng. Hỏi tổng số tiền mà ba an hem trả ở tháng thứ nhất cho ngân hàng là bao nhiêu ( làm tròn đến hàng đơn vị)?

Gọi $n$ là số nguyên dương sao cho $\frac{1}{{{\log }_{3}}x}+\frac{1}{{{\log }_{{{3}^{2}}}}x}+\frac{1}{{{\log }_{{{3}^{3}}}}x}+...+\frac{1}{{{\log }_{{{3}^{n}}}}x}=\frac{210}{{{\log }_{3}}x}$ đúng với mọi $x$ dương. Tìm giá trị của biểu thức $P=2n+3$.

 Tìm tất cả các giá trị của tham số $m$ để hàm số $y=\ln \left( 16{{x}^{2}}+1 \right)-\left( m+1 \right)x+m+2$ nghịch biến trên khoảng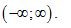  

Tìm tất cả các giá trị thực của tham số m để hệ có nghiệm.

Cho $f\left( n \right)={{\left( {{n}^{2}}+n+1 \right)}^{2}}+\forall n\in \mathbb{N}*.$ Đặt

Tìm số n nguyên dương nhỏ nhất sao cho ${{u}_{n}}$ thỏa mãn điều kiện ${{\log }_{2}}{{u}_{n}}+{{u}_{n}}<-\frac{10239}{1024}.$

Cho x, y là số thực dương thỏa mãn ${{\log }_{2}}x+{{\log }_{2}}y+1\ge {{\log }_{2}}\left( {{x}^{2}}+2y \right).$ Tìm giá trị nhỏ nhất của $P=x+2y$