toán 12 chương 3

Một vật chuyển động theo quy luật    $s\left( t \right)=-\frac{1}{2}{{t}^{3}}+12{{t}^{2}},\,\,t\left( s \right)$ là khoảng thời gian tính từ lúc vật bắt đầu chuyển động, \[s\left( m\acute{e}t \right)\] là quãng đường vật chuyển động trong \[t\] giây. Tính vận tốc tức thời của vật tại thời điểm \[t=10\left( gi\hat{a}y \right).\] 

Cho nửa đường tròn đường kính $AB=4\sqrt{5}.$ Trên đó người ta vẽ một parabol có đỉnh trùng với tâm của nửa hình tròn, trục đối xứng là đường kính vuông góc với AB. Parabol cắt nửa đường tròn tại hai điểm cách nhau 4cm và khoảng cách từ hai điểm đó đến AB bằng nhau và bằng 4cm. Sau đó người ta cắt bỏ phần hình phẳng giới hạn bởi đường tròn và parabol (phần tô màu trong hình vẽ). Đem phần còn lại quay xung quanh trục AB. Thể tích của khối tròn xoay thu được bằng:

 Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số $y=3\text{x}-{{x}^{2}}$ và trục hoành, quanh trục hoành.

Tìm họ nguyên hàm của hàm số \[f\left( x \right) = {e^{2018x}}\]

Tìm mệnh đề sai trong các mệnh đề sau:

Tìm họ nguyên hàm của hàm số $f\left( x \right)={{e}^{2018x}}.$

Tính diện tích hình phẳng giới hạn bởi các đồ thị $y={{x}^{2}}-2x$ và $y=-{{x}^{2}}+x$.

Biết $\int\limits_{0}^{2}{2x\ln \left( x+1 \right)dx=a\ln b,}$ với $a,b\in {{\mathbb{N}}^{*}}$ và b là số nguyên tố. Tính $6a+7b$.

 Biết $\int\limits_{a}^{b}{f(x)\text{d}x=10}$ và \[\int\limits_{a}^{b}{g(x)\text{d}x=5}\]. Tính tích phân $I=\int\limits_{a}^{b}{(3f(x)-5g(x))\text{d}x}$.

Biến đổi $\int\limits_{0}^{3}{\frac{x}{1+\sqrt{1+x}}dx}$ thành $\int\limits_{1}^{2}{f\left( t \right)dt}$ với $t=\sqrt{1+x}.$ Khi đó $f\left( t \right)$ là hàm số nào trong các hàm số sau đây?

Tìm họ nguyên hàm của hàm số $f\left( x \right)=\frac{1}{2\sqrt{2x+1}}.$

Cho số dương a thỏa mãn điều kiện hình phẳng giới hạn bởi các đường parabol \[y=a{{x}^{2}}-2\text{ }v\grave{a}\text{ }y=4-2a{{x}^{2}}\] có diện tích bằng 16. Giá trị của a bằng:

Biết $\int\limits_{1}^{e}{\frac{\ln x}{\sqrt{x}}dx}=a\sqrt{e}+b$ với $a,b\in \mathbb{Z}.$ Tính $P=a.b$ 

Trong các mệnh đề sau, mệnh đề nào sai?

Cho $\int\limits_{-1}^{2}{f\left( x \right)dx=2}$ và $\int\limits_{-1}^{2}{g\left( x \right)dx=-1}.$ Tính $I=\int\limits_{-1}^{2}{\left[ x+2f\left( x \right)-3g\left( x \right) \right]dx}$.

Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ a;b \right]$. Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số  $y=f\left( x \right)$, trục hoành và hai đường thẳng $x=a$, $x=b$ $\left( a

Một vật chuyển động theo quy luật $S=-\frac{1}{2}{{t}^{3}}+3{{t}^{2}}+1,$ với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 4 giây, kể từ lúc vật bắt đầu chuyển động, vận tốc lớn nhất của vật là bao nhiêu ?

Cho hàm số $y=f\left( x \right)$ liên tuc trên $\mathbb{R}$ và thỏa mãn $f\left( 0 \right) < 0 < f\left( -1 \right).$ Gọi S là diện tích hình phẳng giới hạn bởi các đường \[y=f\left( x \right),\text{ }y=0,x=-1\text{ }v\grave{a}\text{ }x=1.\] Xét các mênh đề sau

\[1.\,\,S=\int\limits_{-1}^{0}{f\left( x \right)dx+\int\limits_{0}^{1}{\left| f\left( x \right) \right|dx\,\,\,\,\,\,\,\,\,\,\,\,2.\,\,S=\int\limits_{-1}^{1}{\left| f\left( x \right) \right|dx\,\,\,\,\,\,\,\,\,\,\,3.\,\,S=\int\limits_{-1}^{1}{f\left( x \right)dx\,\,\,\,\,\,\,\,\,\,\,\,4.\,\,S=\left| \int\limits_{-1}^{1}{f\left( x \right)dx} \right|}}}}\]

Số mệnh đề đúng là:

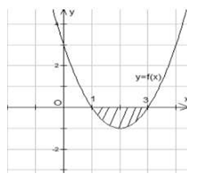
Cho hàm số $y=f\left( x \right)$ liên tục và có đồ thị như hình bên. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục Ox. Quay hình phẳng D quanh trục Ox ta được khối tròn xoay có thể tích V được xác định theo công thức ?

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ \frac{1}{3} \right\}$thỏa mãn $f'\left( x \right)=\frac{3}{3x-1},f\left( 0 \right)=1$ và $f\left( \frac{2}{3} \right)=2.$ Giá trị của biểu thức $f\left( -1 \right)+f\left( 3 \right)$ bằng: