Toán 12 hàm số

Tìm tất cả các giá trị của m để phương trình ${{\sin }^{4}}x+co{{s}^{4}}x+co{{s}^{2}}4x=m$ có bốn nghiệm phân biệt thuộc đoạn $\left[ -\frac{\pi }{4};\frac{\pi }{4} \right].$ 

Cho hàm số $y={{x}^{4}}-2\left( 1-{{m}^{2}} \right){{x}^{2}}+m+1.$ Tìm tất cả các giá trị của tham số m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất.

Tìm m để hàm số \[y=-x{}^{3}-m\text{x}+\frac{3}{28{{\text{x}}^{7}}}\]nghịch biến

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\frac{\sqrt{{{x}^{2}}-1}}{x-2}$ trên cập hợp $D=\left( -\infty ;-1 \right]\cup \left[ 1;\frac{3}{2} \right]$ . Tính giá trị T của m.M

Cho hàm số $y=f(x)$. Hàm số $y={f}'(x)$ có đồ thị như hình bên. Hàm số $y=f\left( 3-2x \right)$ nghịch biến trên khoảng:

Tiếp tuyến với đồ thị \[\left( C \right):y={{x}^{3}}-3{{x}^{2}}-2\] song song với đường thẳng \[\left( d \right):y=9x+3\] có phương trình là:

Hàm số nào dưới đây có đồ thị như hình vẽ

Một trong các đồ thị ở hình vẽ là đồ thị của hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn $f'\left( 0 \right)=0,f''\left( x \right)

Số giá trị nguyên dương của tham số m để hàm số $y={{\left( \frac{1}{2} \right)}^{{{x}^{3}}-6{{\text{x}}^{2}}+m\text{x}+2}}$ luôn đồng biến trên khoảng $\left( 1;3 \right)$ là:

Tìm tất cả các giá trị của tham số m để đồ thị hàm số  $y={{x}^{4}}-2m{{x}^{2}}+2m+{{m}^{4}}$ có 3 điểm cực trị tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 2 lần bán kính đường tròn nội tiếp ?

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ đồng thời hàm số $y=\left| f\left( x \right) \right|$ có đồ thị như hình vẽ bên.

Xác định số cực trị của hàm số $y=f\left( \left| x \right| \right)$

Cho hàm số $y=\frac{x-1}{x+2}$, gọi d là tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng $m-2$. Biết đường thẳng d cắt tiệm cận đứng của đồ thị hàm số tại điểm $A\left( {{x}_{1}};{{y}_{1}} \right)$ và cắt tiệm cận ngang của đồ thị hàm số  tại điểm $B\left( {{x}_{2}};{{y}_{2}} \right)$. Gọi S là tập hợp các số  m sao cho

${{x}_{2}}+{{y}_{1}}=-5$. Tính tổng bình phương các phần tử của S.

Hàm số $f\left( x \right)$liên tục trên R và có đúng ba điểm cực trị là$-2;-1;0$. Hỏi hàm số $y=f\left( {{x}^{2}}-2x \right)$ có bao nhiêu điểm cực trị?

 Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=\frac{m}{3}{{x}^{3}}+7m{{x}^{2}}+14x-m+2$ nghịch biến trên nửa khoảng  ?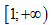

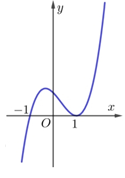
 Cho hàm số $y=f\left( x \right)\left( x-1 \right)$ xác định và liên tục trên $\mathbb{R}$ có đồ thị như hình dưới đây. Tìm tất cả các giá trị của m để đường thẳng $y={{m}^{2}}-m$ cắt đồ thị hàm số $y=f\left( x \right)\left| x-1 \right|$ tại 2 điểm có hoành độ nằm ngoài đoạn $\left[ -1;1 \right].$ 

Cho hàm số $y=f\left( x \right)$ liên tục trên có bảng biến thiên như sau: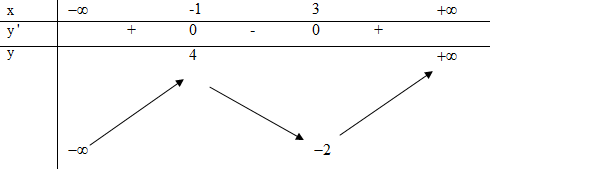

Biết $f\left( 0 \right)

Trong không gian với hệ tọa độ Oxyz, cho điểm $A\left( 1;0;-1 \right)$ và mặt phẳng $\left( P \right):x+y-z-3=0.$ Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng $6+\sqrt{2}.$ Phương trình mặt cầu (S) là:

Cho hàm số $y=-2{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ  thị  như hình dưới. Khẳng định nào sau đây đúng ?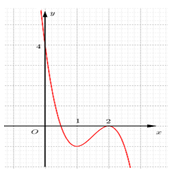 

Cho hàm số $y=f(x)=x+\sqrt{1-{{x}^{2}}}$.Tìm tất cả các giá thực của tham số $m$thỏa mãn$f(x)\le m$ với mọi $x\in \text{ }\!\![\!\!\text{ }-\text{1;1 }\!\!]\!\!\text{ }$.

Tìm tất cả các giá trị của  m  để đồ thị hàm số $y=\left( {{m}^{2}}-1 \right){{x}^{4}}+m{{x}^{2}}+m-2$ chỉ có 1 điểm cực đại và không có điểm cực tiểu.