toán 987654321

Một ô tô đang chạy với tốc độ 10(m/s) thì người lái đạp phanh, từ thời điểm đó ô tô chuyển động chậm dần đều với \[v\left( t \right)=-5t+10\left( m/s \right),\] trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét ?

Tìm họ nguyên hàm của hàm số $f\left( x \right)=\frac{1}{{{\sin }^{2}}x.c\text{o}{{\text{s}}^{4}}x}.$

Biết \[\int\limits_{e}^{{{e}^{4}}}{f\left( \ln x \right)\frac{1}{x}dx}=4\]. Tính tích phân \[I=\int\limits_{1}^{4}{f\left( x \right)dx}\]

Cho F(x) là một nguyên hàm của hàm số $f(x)=\left( 5x+1 \right){{e}^{x}}$ và $F\left( 0 \right)=3.$ Tính F(1).

Cho chuyển động thẳng xác định bởi phương trình \[s=\frac{1}{2}\left( {{t}^{4}}+3{{t}^{2}} \right),\]t được tính bằng giây, s được tính bằng m. Vận tốc của chuyển động tại \[t=4\] ( giây) bằng:

Tìm họ nguyên hàm của hàm số $y=\frac{1}{{{\left( x+1 \right)}^{2}}}$.

Viết công thức tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng vuông góc với Ox tại các điểm $x=a,x=b\,\,\left( a

Họ nguyên hàm của hàm số $f\left( x \right)=\frac{1}{x+1}$ là

Tìm nguyên hàm của hàm số $y={{12}^{12x}}.$ 

Cho parabol $\left( P \right):y={{x}^{2}}+2$ và hai tiếp tuyến của $\left( P \right)$ tại các điểm $M\left( -1;3 \right)$ và $N\left( 2;6 \right).$ Diện tích hình phẳng giới hạn bởi $\left( P \right)$ và hai tiếp tuyến đó bằng:

Tìm nguyên hàm \[F\left( x \right)\] của hàm số \[f\left( x \right)={{e}^{2x}},\] biết \[F\left( 0 \right)=1\].

Tính \[F\left( X \right)=\int{x\cos x}dx\] ta được kết quả

Nếu $\int\limits_{1}^{2}{f\left( x \right)dx=3,\int\limits_{2}^{5}{f\left( x \right)dx=-1}}$ thì $\int\limits_{1}^{5}{f\left( x \right)dx}$ bằng:

Cho $\int\limits_{1}^{2}{f\left( {{x}^{2}}+1 \right)x\,dx=2.}$ Khi đó $I=\int\limits_{2}^{5}{f\left( x \right)dx}$ bằng:

Tính diện tích hình phẳng giới hạn bởi các đồ thị $y={{x}^{2}}-2x$ và $y=-{{x}^{2}}+x$.

Hình phẳng giới hạn bởi đồ thị hàm số \[f\left( x \right)\] liên tục trên đoạn \[\left[ 1;3 \right]\], trục Ox và hai đường thẳng \[x=1;x=3\] có diện tích là:

Tích phân $\int\limits_{0}^{1}{\frac{x-1}{{{x}^{2}}-2x+2}dx}$ bằng:

Một chuyển động thẳng xác định bởi phương trình \[s={{t}^{3}}-3{{t}^{2}}+5t+2\], trong đó t tính bằng giây và s tính bằng mét. Gia tốc của chuyển động khi \[t=3\] là:

Nếu $\int{f\left( x \right)dx}=\frac{1}{x}+\ln \left| 5x \right|+C$ với 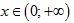 thì hàm số $f\left( x \right)$ là      

Tìm họ nguyên hàm của hàm số $f\left( x \right)={{5}^{x}}$.

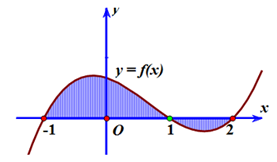
Gọi $S$ là diện tích miền hình phẳng được tô đậm trong hình vẽ dưới đây. Công thức tính $S$ là

Tìm một nguyên hàm F(x) của hàm số $f\left( x \right)=\sin 3x$ thỏa mãn $F\left( \frac{\pi }{2} \right)=2.$ 

Gọi $S$ là diện tích miền hình phẳng được tô đậm trong hình vẽ dưới đây. Công thức tính $S$ là

Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\frac{x+1}{x-2}$ và các trục tọa độ là:

Họ nguyên hàm của hàm số $f\left( x \right)={{x}^{3}}+2x$ là: