ứng dụng đạo hàm

 Tìm tất cả các giá trị thực của m để hàm số \[y=\frac{\cos x-1}{\cos x-m}\] đồng biến trên khoảng \[\left( 0;\frac{\pi }{2} \right).\]

Tìm tất cả các giá trị của m để phương trình ${{\sin }^{4}}x+co{{s}^{4}}x+co{{s}^{2}}4x=m$ có bốn nghiệm phân biệt thuộc đoạn $\left[ -\frac{\pi }{4};\frac{\pi }{4} \right].$ 

Có bao nhiêu giá trị nguyên của \[m\] để hàm số \[f\left( x \right)={{x}^{3}}+3{{x}^{2}}-\left( {{m}^{2}}-3m+2 \right)x+5\] đồng biến trên \[\left( \text{ }0;2\text{ } \right)\text{ }?\] 

Tìm tất cả các giá trị của m để hàm số $y=\frac{mx+3}{x+2}$ nghịch biến trên từng khoảng xác định của nó.

Cho hàm số $y={{x}^{4}}-2\left( 1-{{m}^{2}} \right){{x}^{2}}+m+1.$ Tìm tất cả các giá trị của tham số m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất.

Cho hàm số $y=f\left( x \right)$ có bảng thiến thiên như sau:

Hàm số đạt cực tiểu tại điểm nào?

Hàm số $f\left( x \right)$ có đạo hàm $f'\left( x \right)$ trên khoảng $\text{K}$. Hình vẽ bên là đồ thị của hàm số $f'\left( x \right)$ trên khoảng $\text{K}$. Số điểm cực trị của hàm số đã cho là

Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số $y=\left| {{x}^{2}}+2x+m-4 \right|$ trên đoạn $\left[ -2;1 \right]$ bằng 4?

Cho hàm số có đồ thị (C): $y=\frac{2x+1}{x-1}$. Gọi M là điểm bất kì thuộc đồ thị (C). Gọi tiếp tuyến của đồ thị (C) tại M cắt các tiệm cận của (C) tại hai điểm P và Q. Gọi G là trọng tâm tam giác IPQ (với I là giao điểm của hai đường tiệm cận của (C)). Diện tích tam giác GPQ là

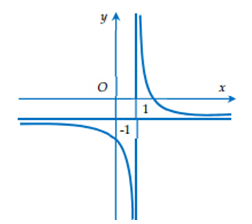
Cho hàm số \[y=\frac{ax-b}{x-1}\] có đồ thị như hình dưới. Khẳng định nào dưới đây là đúng?