Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của khối chóp tam giác S.ABC sao cho $\frac{SM}{MA}=\frac{1}{2};\frac{SN}{NB}=2.$ Mặt phẳng 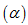đi qua MN và song song với SC chia khối chóp thàng 2 phần. Gọi \[{{V}_{1}}\] là thể tích của khối đa diện chứa \[A,\text{ }{{V}_{2}}\] là thể tích của khối đa diện còn lại. Tính tỉ số $\frac{{{V}_{1}}}{{{V}_{2}}}$.