Cho khối chóp \[S.ABC\] có \[SA=SB=SC=a\] và \[ASB=BSC=CSA={{30}^{\circ }}.\] Mặt phẳng 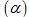qua A và cắt hai cạnh \[SB,\text{ }SC\] tại B’, C’ sao cho chu vi tam giác \[ABC\] nhỏ nhất. Tính $k=\text{ }\frac{{{V}_{S.A'B'C'}}}{{{V}_{S.ABC}}}$