chậc 12345 hehehe

Cho các phát biểu sau

(a) Thủy phân vinyl axetat bằng NaOH đun nóng, thu được natri axetat và axetanđehit.

(b) Ở điều kiện thường, các este đều là những chất lỏng.

(c) Amilopectin và xenlulozo đều có cấu trúc mạch phân nhánh.

(d) Phản ứng xà phòng hóa chất béo luôn thu được các axit béo và glixerol .

(e) Glucozo là hợp chất hữu cơ đa chức.

(g) Tinh bột và xenlulozơ đều không bị thủy phân trong môi trường kiềm.

Số phát biểu đúng là

Tìm hệ góc k của tiếp tuyến của đồ thị hàm số \[y=\frac{x}{x+1}\] tại điểm \[M\left( -2;2 \right)\].

Giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=x+1+\sqrt{4-{{x}^{2}}}$  lần lượt là M và m, chọn câu trả lời đúng.

Tìm khoảng đồng biến của hàm số \(y=ln\left ( \sqrt{x}-1 \right )\)

Este X đơn chức, mạch hở có khối lượng oxi chiếm 32% . Đốt cháy hoàn toàn 0,2 mol hỗn hợp E gồm X và 2 este Y, Z (đều no, mạch hở, MY < MZ) thu được 0,7 mol CO2 và 0,625 mol H2O. Biết E phản ứng với dung dịch KOH vừa đủ chỉ thu được hỗn hợp hai ancol (có cùng số nguyên tử cacbon) và hỗn hợp hai muối. Thành phần % số mol của Z trong E là

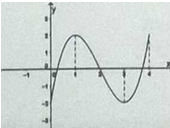
Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ 0;4 \right]$ có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng ?

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số: \[y=2{{\sin }^{2}}x-\cos x+1.\] Giá trị \[M+m\] bằng: 

Biết đồ thị hàm số \[y={{x}^{4}}+b{{x}^{2}}+c\] chỉ có một điểm cực trị là điểm có tọa độ \[\left( 0;-1 \right)\] thì b và c thỏa mãn điều kiện nào ?

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình dưới đây:

I. Hàm số đồng biến trên khoảng $\left( -3;-2 \right).$

II. Hàm số đồng biến trên khoảng $\left( -\infty ;5 \right).$

III. Hàm số nghịch biến trên khoảng

IV. Hàm số đồng biến trên khoảng $\left( -\infty ;-2 \right).$

Số mệnh đề sai trong các mệnh đề trên là:

Giá trị lớn nhất của hàm số $y=\frac{1}{3}{{x}^{3}}-2{{x}^{2}}+3x-4$ trên đoạn $\left[ 1;5 \right]$ là?