chậc 12345 hehehe

Bảng biến thiên dưới đây là của hàm số nào ?

Biết ${{m}_{0}}$ là giá trị của tham số m để hàm số $y={{x}^{3}}-3{{x}^{2}}+mx-1$ có hai điểm cực trị ${{x}_{1}},{{x}_{2}}$ sao cho $x_{1}^{2}+x_{2}^{2}-{{x}_{1}}{{x}_{2}}=13.$ Mệnh đề nào dưới đây đúng ?

Số điểm cực trị của hàm số \[y=-{{x}^{3}}+3{{x}^{2}}+x+1\] là

Tìm tất cả giá trị của m để phương trình ${{x}^{3}}-3x-m+1=0$ có ba nghiệm phân biệt.

Cho đồ thị của hàm số $y={{x}^{3}}-3{{x}^{2}}+1$ như hình vẽ.

Khi đó, phương trình ${{x}^{3}}-3{{x}^{2}}+1=m$ ($m$ là tham số ) có $3$ nghiệm phân biệt khi và chỉ khi:

Tìm tiệm cận ngang của đồ thị hàm số\[y=\frac{1-x}{x+2}.\]

Khoảng cách giữa hai tiệm cận đứng của đồ thị hàm số \[y=\frac{1}{{{x}^{2}}-2}\] bằng:

Đường thẳng $y=1$ cắt đồ thị hàm số $y={{x}^{3}}-3{{x}^{2}}+2x+1$ tại ba điểm phân biệt $M,N,P$biết $N$ nằm giữa $M$ và $P$. Tính độ dài $MP.$

Tìm giá trị lớn nhất của hàm số \[y={{x}^{3}}-3{{x}^{2}}-9x+1\] trên đoạn \[\left[ 0;4 \right]\]. 

Tìm GTLN của hàm số \[y=\sqrt{5-{{x}^{2}}}\] trên\[\left[ -\sqrt{5};\sqrt{5} \right]\] ?

Tìm tập hợp S tất cả các giá trị của tham số thực m để hàm số \[y=\frac{{{x}^{3}}}{3}+m{{x}^{2}}+\left( 2m+3 \right)x+1\] đồng biến trên R.

Lên men hoàn toàn a gam glucozo, thu đuợc C2H5OH và CO2. Hấp thụ hết CO2 sinh ra vào dung dịch nuớc vôi trong dư, thu đuợc 15 gam kết tủa. Giá trị của a là:

Đốt cháy hoàn toàn m gam hỗn hợp X gồm 2 este đồng phân cần dùng 4,704 lít khí O2, thu được 4,032 lít CO2 và 3,24 gam H2O. Nếu cho m gam X tác dụng hết với 110 mL dung dịch KOH 1M. Cô cạn dung dịch sau phản ứng thì thu được 7,98 gam chất rắn khan, trong đó có a mol muối Y và b mol muối Z (MY > MZ). Các thể tích khí đều đo ở điều kiện tiêu chuẩn. Tỉ lệ a : b là:

Đồ thị hàm số nào dưới đây đi qua điểm \[M\left( 2;-1 \right)\] ? 

Cho hàm số \[y=f\left( x \right)=a{{x}^{4}}+{{b}^{2}}{{x}^{2}}+1\left( a\ne 0 \right).\] Trong các khẳng định dưới đây, khẳng định nào là đúng ?

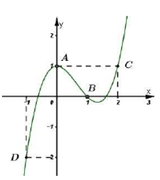
Cho hàm số \[y=f\left( x \right)\]với đạo hàm \[f'\left( x \right)\] có đồ thị như hình vẽ. Hàm số \[g\left( x \right)=f\left( x \right)-\frac{{{x}^{3}}}{3}+{{x}^{2}}-x+2\] đạt cực đại tại điểm nào ? 

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số $y=\frac{{{x}^{2}}}{2}-mx+\ln (x-1)$ đồng biến trên khoảng $(1;+\infty )?$

Hỏi có bao nhiêu giá trị m nguyên trong đoạn \[\left[ -2017;2017 \right]\] để hàm số \[y={{x}^{3}}-3\left( 2m+1 \right){{x}^{2}}+\left( 12m+5 \right)x-2\] đồng biến trên khoảng ?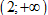 

Cho hàm số $y=f\left( x \right)$có bảng biến thiên như hình vẽ bên. Hàm số $y=2f\left( x \right)$ đạt cực đại tại

Cho hàm số \[y=\frac{x+2}{x-2}\] có đồ thị \[\left( C \right)\]. Gọi \[I\] là giao điểm hai đường tiệm cận của \[\left( C \right)\]. Tiếp tuyến của \[\left( C \right)\] cắt hai đường tiệm cận của \[\left( C \right)\] tại hai điểm \[A,B\]. Giá trị nhỏ nhất của chu vi đường tròn ngoại tiếp tam giác \[IAB\] bằng