chậc 12345 hehehe

Tìm số tiệm cận đứng của đồ thị hàm số $y=\frac{{{x}^{2}}-3x-4}{{{x}^{2}}-16}.$

Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\frac{1}{x}-3$ là.

Có bao nhiêu giá trị nguyên của m để hàm số \[f(x)=2{{x}^{3}}-6{{x}^{2}}-m+1\] có các giá trị cực trị trái dấu?

Cho đồ thị (C): $y=\frac{x+2}{x-1}$, tiếp tuyến với đồ thị (C ) tại một điểm bất kì thuộc (C ) luôn tạo với hai đường tiệm cận của (C ) một tam giác có diện tích không đổi. Diện tích đó bằng:

Tập hợp các giá trị của tham số m sao cho đồ thị hàm số $y=\frac{{{m}^{2}}x+1}{x-1}$ có tiệm cận ngang đường thẳng $y=4$

Cho hàm số \[y=f(x)\]. Mệnh đề nào sau đây đúng ?

Biết đồ thi ̣(C) của hàm số $y=\frac{{{x}^{2}}-2x+3}{x-1}$ có hai điểm cực trị. Đường thẳng đi qua hai điểm cực tri ̣của đồ thi ̣(C) cắt trục hoành tại điểm M có hoành độ ${{x}_{M}}$ bằng:

Cho hàm số $y=\frac{mx+3}{4x-2n+5}$. Đồ thị hàm số có phương trình TCN $y=2$ và nhận trục tung làm tiệm cận đứng. Khi đó $m+n$ bằng:

Hàm số nào sau đây nghịch biến trên $\mathbb{R}$ .

Hàm số $y={{x}^{3}}+3{{x}^{2}}-4$ nghịch biến trên khoảng nào sau đây? 

Đồ thị hàm số $y=\frac{2x-7}{x-3}$ có tiệm cận đứng là đường thẳng?

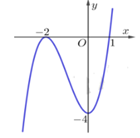
Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên. Hàm số $y=f\left( x \right)$ nghịch biến trên khoảng nào dưới đây?

Một con lắc đơn có chiều dài l dao động điều hòa tại nơi có gia tốc trọng trường . Khi tăng chiều dài của con lắc đơn thêm một đoạn 3l .Thì chu kì dao động riêng của con lắc

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \[y={{x}^{3}}+3{{x}^{2}}-9x+1\] trên đoạn \[\left[ -4;4 \right]\] Tổng \[M+m\] bằng

Cho hàm số \[y=f\left( x \right)\] có đạo hàm trên . Phát biểu nào sau đây là đúng ?