chậc 123hehehehehehe

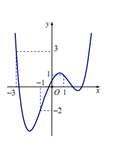
Cho hàm số $y=f\left( x \right)$ có đồ thị $y=f'\left( x \right)$ như hình vẽ. Xét hàm số $g\left( x \right)=f\left( x \right)-\frac{1}{3}{{x}^{3}}-\frac{3}{4}{{x}^{2}}+\frac{3}{2}x+2018.$ Mệnh đề nào dưới đây đúng ?

Cho hàm số $y={{x}^{4}}-m{{x}^{2}}+m$ với m là tham số, có đồ thị là $\left( C \right)$. Biết rằng đồ thị $\left( C \right)$ cắt trục hoành tại 4 điểm phân biệt có hoành độ ${{x}_{1}},\,{{x}_{2}},\,{{x}_{3}},$ thỏa mãn ${{x}_{4}}x_{1}^{4}+x_{2}^{4}+x_{3}^{4}+x_{4}^{4}=30$ khi $m={{m}_{0}}.$ Hỏi mệnh đề nào sau đây là đúng ?

Cho hàm số$f\left( x \right)$xác định trên R và hàm số $y=f'\left( x \right)$có đồ thị như hình bên dưới:

Xét các khẳng định sau:

(I) Hàm số$y=f\left( x \right)$có ba cực trị.

(II) Phương trình $f\left( x \right)=m+2018$có nhiều nhất ba nghiệm.

(III) Hàm số$y=f\left( x+1 \right)$nghịch biến trên khoảng $\left( 0;1 \right)$.

Số khẳng định đúng là: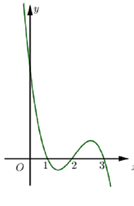                    

Cho phương trình ${{x}^{12}}+1=4{{x}^{4}}\sqrt{{{x}^{n}}-1}.$ Tìm số nguyên dương n bé nhất để phương trình có nghiệm.

Tính số nghiệm của phương trình \[\cot x={{2}^{x}}\] trong khoảng \[\left( \frac{11\pi }{12};2019\pi \right)\].