Đê 124213213213214321421

Gọi S là tập hợp các giá trị thực của tham số m để hàm số $y={{x}^{3}}-3m{{x}^{2}}+4{{m}^{3}}$ có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 (O là gốc tọa độ). Ta có tổng giá trị tất cả các phần tử của tập S bằng:

Cho hàm số \[y={{x}^{3}}+3{{x}^{2}}-9x+1.\] Mệnh đề nào dưới đây đúng ? 

Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ 0;4 \right]$ có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng ?

Phân tích este X người ta thu được kết quả %C= 40%; %H = 6,66. Este X là

Cho hàm số $y=f\left( x \right)$ có đạo hàm $y={f}'\left( x \right)$ liên tục trên $\mathbb{R}$ và đồ thị của hàm số ${f}'\left( x \right)$ trên đoạn \[\left[ -2;6 \right]\] như hình vẽ bên.

Tìm khẳng định đúng trong các khẳng định sau.

Hai điện tích q1 = q2 = 4.10-10 C đặt tại hai điểm A và B cách nhau một khoảng a = 10 cm trong không khí. Độ lớn lực điện mà q1 và q2 tác dụng lên q3 = 3.10-12 C đặt tại C cách A và B những khoảng bằng a là

Đồ thị hàm số \[y={{x}^{3}}+2{{x}^{2}}+5x+1\] và đường thẳng \[y=3\text{x }+1\] cắt nhau tại điểm duy nhất $\left( {{x}_{0}};{{y}_{0}} \right)$ khi đó:

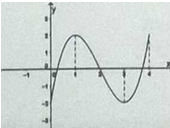
Hàm số $y=f(x)$ với đồ thị như hình vẽ có bao nhiêu điểm cực trị?

Protein tham gia phản ứng màu biure tạo thành dung dịch có màu.

Hàm số \[y={{x}^{4}}+m{{x}^{2}}-m-5\] (\[m\] là tham số) có 3 điểm cực trị khi các giá trị của \[m\] là: 

Đồ thị hàm số nào sau đây không có tiệm cận ngang ?

Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)={{x}^{2}}\left( x-1 \right)\left( {{x}^{2}}-4 \right).$ Số điểm cực trị của hàm số $y=f\left( x \right)$ là:

Hàm số \[y=\sqrt{{{x}^{2}}-4x+3}\] nghịch biến trên khoảng nào trong các khoảng sau ?

Cho hàm số \[y=\frac{ax-4}{x+b}\] có đồ thị \[\left( C \right).\] Đồ thị \[\left( C \right)\] nhận đường thẳng \[x=2\] làm tiệm cận đứng và \[\left( C \right).\] đi qua điểm \[A\left( 4;2 \right)\]. Tính giá trị của biểu thức \[P=a+b.\]

Cho hàm số: $y=-\frac{{{x}^{3}}}{3}+\left( a-1 \right){{x}^{2}}+\left( a+3 \right)x-4.$ Tìm \[a\] để hàm số đồng biến trên khoảng \[\left( 0;3 \right)\] .

Giá trị nhỏ nhất của hàm số \[y=-x+\sqrt{2{{x}^{2}}+1}\] là:

Các đường tiệm cận của đồ thị hàm số $y=\frac{2x+1}{x-1}$ là

Đường cong ở hình bên là đồ thị của hàm số nào sau đây ?

Tìm tất cả các giá trị của m để phương trình \[{{x}^{4}}-2{{x}^{2}}-m=0\] có bốn nghiệm phân biệt. 

Hỗn hợp X chứa 1 ancol đơn chức (A), axit hai chức (B) và este 2 chức (D) đều no, hở và có tỉ lệ mol tương ứng 3:2:3. Đốt cháy hoàn toàn m gam hỗn hợp X cần dùng 6,272 lít O2 (đktc). Mặt khác đun nóng m gam hỗn hợp X trong 130 ml dung dịch NaOH 1M thu được dung dịch Y và hỗn hợp 2 ancol là đồng đẳng kế tiếp. Cô cạn dung dịch Y sau đó nung với CaO thu được duy nhất một hidrocacbon đơn giản nhất có khối lượng 0,24 gam. Các phản ứng đạt hiệu suất 100%. CTPT có thể có của ancol là

Một trong các đồ thị ở hình vẽ là đồ thị của hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn $f'\left( 0 \right)=0,f''\left( x \right)

Cho đường cong $\left( C \right)$ có phương trình $y=\frac{x-1}{x+1}$. Gọi $M$ là giao điểm của  $\left( C \right)$ với trục tung. Tiếp tuyến của $\left( C \right)$ tại $M$ có phương trình là

Cho hàm số $y=f\left( x \right)$ có đồ thị $y=f'\left( x \right)$ cắt trục Ox tại 3 điểm có hoành độ $a

Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right)=\frac{{{x}^{2}}-3x+6}{x-1}$ trên đoạn $\left[ 2;4 \right]$ lần lượt là $M,\,\,m$. Tính $S=M+m$. 

Hàm số nào dưới đây có đồ thị như hình vẽ

Cho hàm số $y=f(x)$ xác định và liên tục trên $\mathbb{R}$  có  $f(x)>0\text{ }\forall x\in \mathbb{R}$, $f(0)=1$ Biết $\frac{f'(x)}{f(x)}=2-2x$, tìm tất cả các giá trị của m để phương trình $f(x)=m$ có 2 nghiệm thực phân biệt.

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=\frac{1}{3}{{x}^{3}}-\frac{1}{2}m{{x}^{2}}+2mx-3m+4$ nghịch biến trên đoạn có độ dài là 3?

Cho hàm số $y=f\left( x \right)$ có bảng thiến thiên như sau:

Hàm số đạt cực tiểu tại điểm nào?

Giá trị nhỏ nhất m và giá trị lớn nhất M  của hàm số $y=\frac{\sin x+2\cos x+1}{sinx+\cos x+2}$ là:

Biết hàm số \[y=\left( x+m \right)\left( x+n \right)\left( x+p \right)\] không có cực trị. Giá trị nhỏ nhất của \[F={{m}^{2}}+2n-6p\] là:

Cho a, b, c là các số thực, theo thứ tự lập thành cấp số nhân

Có tất cả bao nhiêu giá trị nguyên của m để hàm số $y=\frac{x+2}{x+3m}$ đồng biến trên $\left( -\infty ;-6 \right)$?

 Cho hàm số $y=f\left( x \right)$ có đồ thị $y=f'\left( x \right)$ cắt trục Ox tại ba điểm có hoành độ $a

Gọi \[d\] là đường thẳng đi qua \[A\text{ }\left( 2;0 \right)\] có hệ số góc \[m\] cắt đồ thị $\left( C \right):y=-{{x}^{3}}+6{{x}^{2}}-9x+2$ tại ba điểm phân biệt \[A,\text{ }B,\text{ }C.\] Gọi \[B',\text{ }C'\] lần lượt là hình chiếu vuông góc của \[B,\text{ }C\] lên trục tung. Tìm giá trị dương của \[m\] để hình thang \[BB'C'C\]  có diện tích bằng \[8.\] 

Cho hàm số \[f\left( x \right)\] có đạo hàm trên \[R\] và có đồ thị hàm \[y=\text{ }f'\left( x \right)\] như hình vẽ. Xét hàm số \[g\left( x \right)=f\left( {{x}^{2}}-2 \right).\] Mệnh đề nào dưới đây sai ?

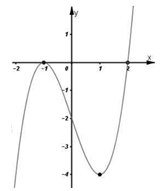
Gọi \[S\]là tập hợp tất cả các giá trị nguyên dương của tham số thực \[m\]sao cho hàm số $y=\frac{{{x}^{4}}}{4}-\frac{3}{2}m{{x}^{2}}+2x+\frac{2}{{{x}^{2}}}$ đồng biến trên nửa khoảng 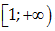. Số phần tử của tập \[S\] là

Cho hàm số $y=f\left( x \right)=\frac{ax+b}{cx+d}$ có đồ thị hàm số $f'\left( x \right)$  như trong hình vẽ bên.

Biết rằng đồ thị hàm số $f\left( x \right)$ đi qua điểm $A\left( 0;4 \right).$ Khẳng định nào dưới đây là đúng?

Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right)=\frac{{{x}^{2}}-3x+6}{x-1}$ trên đoạn $\left[ 2;4 \right]$ lần lượt là $M,\,\,m$. Tính $S=M+m$. 

Cho đường cong $\left( C \right)$ có phương trình $y=\frac{x-1}{x+1}$. Gọi $M$ là giao điểm của  $\left( C \right)$ với trục tung. Tiếp tuyến của $\left( C \right)$ tại $M$ có phương trình là

Cho hàm số x = f(x) xác định trên R và có đồ thị hàm số như hình vẽ. Mệnh đề nào sau đây là đúng?