đề đề đề đề đề đề 111111112

Số giá trị nguyên của tham số $m$ để phương trình $\sqrt[3]{m-x}+\sqrt{2x-3}=4$ có ba nghiệm phân biệt là:

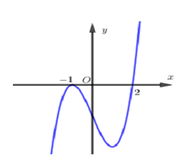
Cho các số thực a, b, c thỏa mãn . Tìm số giao điểm của đồ thị hàm số $y={{x}^{3}}+a{{x}^{2}}+bx+c$ và trục Ox.

Gọi S là tập các giá trị dương của tham số m sao cho hàm số \[y={{x}^{3}}-3m{{x}^{2}}+27x+3m-2\] đạt cực trị \[{{x}_{1}},{{x}_{2}}\] thỏa mãn \[\left| {{x}_{1}}-{{x}_{2}} \right|\le 5\]. Biết S = (a;b]. Tính T = 2b - a.

Cho hàm số y = f (x) có đồ thị $y=f'(x)$ như hình vẽ bên dưới. Đồ thị hàm số $g(x)=\left| 2f(x)-{{(x-1)}^{2}} \right|$ có tối đa bao nhiêu điểm cực trị ?

Tìm tất cả  các giá trị  thực của tham số  a để  hàm số $y={{x}^{3}}-27ax$ có cực đại, cực tiểu và đường thẳng đi qua cực đại và cực tiểu của đồ thị hàm số đi qua gốc tọa độ :

Cho hàm số $f\left( x \right)$có đạo hàm trên $\mathbb{R}$và có đồ thị hàm $y=f'\left( x \right)$ như hình vẽ. Xét hàm số $g\left( x \right)=f\left( {{x}^{2}}-2 \right)$. Mệnh đề nào dưới đây sai?

Cho hàm số bậc ba $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị như hình vẽ bên dưới:

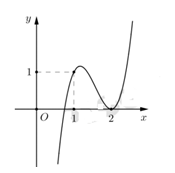
Hỏi đồ thị hàm số $g\left( x \right)=\frac{\left( {{x}^{2}}-3x+2 \right)\sqrt{x-1}}{x\left[ {{f}^{2}}\left( x \right)-f\left( x \right) \right]}$ có bao nhiêu đường tiệm cận đứng ?

Tìm tất cả các giá trị của m để hàm số $y=(m-3)x-(2m+1)cosx$ nghịch biến trên tập xác định.

Xét hàm số \[f\left( x \right)=\left| {{x}^{2}}+ax+b \right|,\] với a, b là tham số. Gọi M là giá trị lớn nhất của hàm số trên \[\left[ -1;3 \right].\] Khi M nhận giá trị nhỏ nhất có thể được, tính \[a+2b.\]

Biết đồ thị hàm số $f\left( x \right)=a\,{{x}^{3}}+b{{x}^{2}}+cx+d$ cắt trục hoành tại ba điểm phân biệt có hoành độ lần lượt là ${{x}_{1}},{{x}_{2}},{{x}_{3}}.$ Tính giá trị của biểu thức $T=\frac{1}{f'\left( {{x}_{1}} \right)}+\frac{1}{f'\left( {{x}_{2}} \right)}+\frac{1}{f'\left( {{x}_{3}} \right)}.$

Cho x, y là những số thực thỏa mãn $x^{2}-xy+y^{2}=1$. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $P=\frac{x^{4}+y^{4}+1}{x^{2}+y^{2}+1}$. Giá trị của A = M + 15m là

Một màn ảnh hình chữ nhật cao 1,4m được đặt ở độ cao 1,8m so với tầm mắt (tính đầu mép dưới của màn hình). 

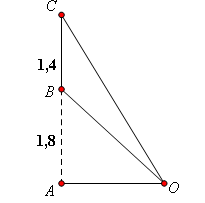
Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác định khoảng cách đó. 

Cho hàm số \[y=\frac{12+\sqrt{4x-{{x}^{2}}}}{\sqrt{{{x}^{2}}-6x+2m}}\]có đồ thị \[\left( {{C}_{m}} \right)\]. Tìm tập S tất cả các giá trị của tham số thực m để \[\left( {{C}_{m}} \right)\]có đúng hai tiệm cận đứng.

Có bao nhiêu giá trị nguyên của tham số m để phương trình$\sin 2x+cos2x+\left| \sin x+cosx \right|-\sqrt{co{{s}^{2}}x+m}-m=0$ có nghiệm thực?

Cho hàm số $y = \frac{{{x^3}}}{3} - a{x^2} - 3ax + 4,$ với a là tham số. Để hàm số đạt cực trị tại ${x_1},{x_2}$ thỏa mãn $\frac{{x_1^2 + 2a{x_2} + 9a}}{{{a^2}}} + \frac{{{a^2}}}{{x_2^2 + 2a{x_1} + 9a}} = 2$ thì a thuộc khoảng nào?

Cho \[x,\text{ }y\] thỏa mãn $\sqrt{2x+3}+\sqrt{y+3}=4.$ Tìm giá trị nhỏ nhất của $P=\sqrt{x+2}+\sqrt{y+9}$.

Tìm tất cả các giá trị thực của tham số m sao cho phương trình

 có hai nghiệm thực phân biệt

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}.$ Đồ thị của hàm số $y=f'\left( x \right)$ như hình bên. Đặt $g\left( x \right)=2f\left( x \right)-{{\left( x+1 \right)}^{2}}.$ Mệnh đề nào dưới đây đúng ?

Biết hàm số $f\left( x \right)-f\left( 2x \right)$ có đạo hàm bằng 18 tại $x=1$ và đạo hàm bằng 1000 tại $x=2$. Tính đạo hàm của hàm số $f\left( x \right)-f\left( 4x \right)$ tại $x=1$.

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên R. Bảng biến thiên của hàm số $y=f'\left( x \right)$ được cho như hình vẽ bên. Hàm số $y=f\left( 1-\frac{x}{2} \right)+x$ nghịch biến trên khoảng ?