đề kiểm tra 15p lần cuối 2018

Gọi A, B là hai điểm cực trị của đồ thị hàm số $f\left( x \right)=-{{x}^{3}}+3x-4$ và \[M\left( {{x}_{0}};0 \right)\] là điểm trên trục hoành sao cho tam giác MAB có chu vi nhỏ nhất, đặt \[T=4{{x}_{0}}+2015.\] Trong các khẳng định dưới đây, khẳng định nào đúng ?

Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số $y=\left( m+1 \right){{x}^{3}}+\left( m+1 \right){{x}^{2}}-2x+2$ nghịch biến trên $\mathbb{R}$.

Cho hàm số \[y={{x}^{4}}-4{{x}^{2}}+3\] có đồ thị như hình vẽ. Tìm số cực trị của hàm số \[y=\left| {{x}^{4}}-4{{x}^{2}}+3 \right|\].

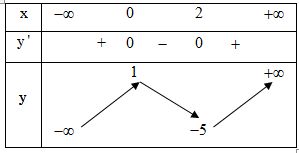
 Cho hàm số $y=f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình bên. Tìm số nghiệm của phương trình $3\left| f\left( x \right) \right|-7=0.$ 

Cho hàm số \[y=f(x)\]xác định trên khoảng (-∞;+∞) và có \[f'(x)=x({{x}^{2}}-1)\].Hàm số \[y=f(x)\]nghịch biến trên mỗi khoảng nào ?

Cho hàm số $y=x\left( {{x}^{2}}-3 \right)$ có đồ thị $\left( C \right)$. Có bao nhiêu điểm M thuộc đồ thị $\left( C \right)$ thỏa mãn tiếp tuyến tại M của $\left( C \right)$cắt $\left( C \right)$và trục hoành lần lượt tại hai điểm phân biệt A (khác M) và B sao cho M là trung điểm của đoạn thẳng AB?

Cho hàm số \[y=f\left( x \right)\] xác định, liên tục và có đạo hàm trên đoạn \[\left[ a,b \right].\] Xét các khẳng định sau:

1. Hàm số \[f\left( x \right)\] đồng biến trên \[\left( a;b \right)\] thì \[f'\left( x \right)>0,\forall x\in \left( a;b \right)\]

2. Giả sử \[f\left( a \right)>f\left( c \right)>f\left( b \right),\forall x\in \left( a;b \right)\] suy ra hàm số nghịch biến trên \[\left( a;b \right)\]

3. Giả sử phương trình\[f'\left( x \right)=0\] có nghiệm là \[x=m\] khi đó nếu hàm số \[y=f\left( x \right)\] đồng biến trên \[\left( m;b \right)\] thì hàm số \[y=f\left( x \right)\] nghịch biến trên \[\left( a,m \right)\]

4. Nếu \[f'\left( x \right)\ge 0,\forall x\in \left( a;b \right)\], thì hàm số đồng biến trên \[\left( a;b \right)\]

Số khẳng định đúng trong các khẳng định trên là:

Cho phương trình ${{x}^{3}}-3{{x}^{2}}+1-m=0\left( 1 \right).$ Điều kiện của tham số m để phương trình (1) có ba nghiệm phân biệt thỏa mãn ${{x}_{1}}

Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ bên. Phương trình $\left| f\left( x-2 \right)-2 \right|=\pi $ có bao nhiêu nghiệm thực phân biệt ?

Tìm tất cả các giá trị của m để hàm số $y=\left( m-1 \right){{x}^{3}}-3\left( m-1 \right){{x}^{2}}+3\text{x}+2$ đồng biến trên $\mathbb{R}$.