Đề kiểm tra chương 1

Tìm điều kiện của a và b để hàm số \(y=asinx+bcosx+x\) đồng biến trên tập xác định.

Cho hàm số \[y=\frac{12+\sqrt{4x-{{x}^{2}}}}{\sqrt{{{x}^{2}}-6x+2m}}\]có đồ thị \[\left( {{C}_{m}} \right)\]. Tìm tập S tất cả các giá trị của tham số thực m để \[\left( {{C}_{m}} \right)\]có đúng hai tiệm cận đứng.

Gọi $S$ là tập các giá trị của tham số thực $m$ để hàm số $y={{x}^{2}}+\ln \left( x+m+2 \right)$ đồng biến trên tập xác định của nó. Biết $S=\left( -\infty ;a+\sqrt{b} \right]$. Tính tổng $K=a+b$ là 

Cho hàm số y = f (x) có đồ thị $y=f'(x)$ như hình vẽ bên dưới. Đồ thị hàm số $g(x)=\left| 2f(x)-{{(x-1)}^{2}} \right|$ có tối đa bao nhiêu điểm cực trị ?

Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y={{e}^{\frac{3x-\sqrt{m{{x}^{2}}+1}}{x-\sqrt{\left( 2018-m \right){{x}^{2}}+1}}}}$ có 2 tiệm cận ngang?

Cho hàm số $g\left( x \right)=\left( 1+x+\frac{{{x}^{2}}}{2!}+\frac{{{x}^{3}}}{3!}+...+\frac{{{x}^{n}}}{n!} \right)\left( 1-x+\frac{{{x}^{2}}}{2!}-\frac{{{x}^{3}}}{3!}+...-\frac{{{x}^{n}}}{n!} \right)$ với $x>0$ và n là số nguyên dương lẻ $\ge $ 3. Mệnh đề nào dưới đây đúng?

Cho hàm số $f\left( x \right)$có đạo hàm trên $\mathbb{R}$và có đồ thị hàm $y=f'\left( x \right)$ như hình vẽ. Xét hàm số $g\left( x \right)=f\left( {{x}^{2}}-2 \right)$. Mệnh đề nào dưới đây sai?

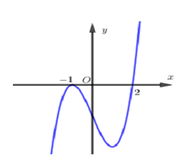
Cho hàm số$f\left( x \right)$xác định trên R và hàm số $y=f'\left( x \right)$có đồ thị như hình bên dưới:

Xét các khẳng định sau:

(I) Hàm số$y=f\left( x \right)$có ba cực trị.

(II) Phương trình $f\left( x \right)=m+2018$có nhiều nhất ba nghiệm.

(III) Hàm số$y=f\left( x+1 \right)$nghịch biến trên khoảng $\left( 0;1 \right)$.

Số khẳng định đúng là: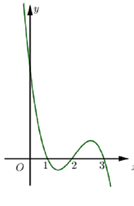                    

Cho hàm số $y=f\left( x \right)$có bảng biến thiên như sau.

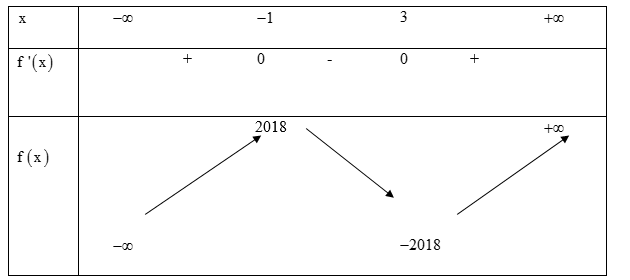
Đồ thị hàm số \[y=\left| f\left( \text{x}-2017 \right)+2018 \right|\] có bao nhiêu điểm cực trị?

Gọi ${{k}_{1}};{{k}_{2}};{{k}_{3}}$ lần lượt là hệ số góc của tiếp tuyến của đồ thị các hàm số $y=f\left( x \right);\,\,y=\left( x \right);\,\,y=\frac{f\left( x \right)}{g\left( x \right)}$ tại $x=2$ và thỏa mãn ${{k}_{1}}={{k}_{2}}=2{{k}_{3}}\ne 0$ khi đó:

Cho hàm số $y=f\left( x \right)\left( x-1 \right)$liên tục trên $\mathbb{R}$và có đồ thị như hình vẽ.

Tìm tất cả các giá trị của tham số m để phương trình $f\left( x \right)\left| x-1 \right|=m$ có số nghiệm lớn nhất.

Tìm tất cả các giá trị của m để hàm số \(y=\frac{mx+1}{x+m}\)  đồng biến trên khoảng \(\left ( -2;+\infty \right )\)

Tìm $m$ để phương trình ${{2}^{\left| x \right|}}=\sqrt{{{m}^{2}}-{{x}^{2}}}$ có 2 nghiệm phân biệt

Cho hàm số $f\left( x \right)={{x}^{3}}+3{{x}^{2}}+mx+1.$ Gọi S là tổng tất cả giá trị của tham số m để đồ thị hàm số $y=f\left( x \right)$ cắt đường thẳng $y=1$ tại ba điểm phân biệt $A\left( 0;1 \right), B, C$ sao cho các tiếp tuyến của đồ thị hàm số $y=f\left( x \right)$ tại B, C vuông góc với nhau. Giá trị của S bằng:

Cho hàm số $f\left( x \right)$ có đồ thị hàm số $y=f'\left( x \right)$

được cho như hình vẽ bên. Hàm số $y=f\left( \operatorname{cosx} \right)+{{x}^{2}}-x$

đồng biến trên khoảng:

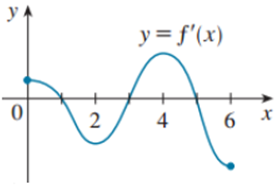
Cho hàm số $y = f\left( x \right)$ liên tục và có đạo hàm trên $\left[ {0;6} \right].$ Đồ thị của hàm số $y = f'\left( x \right)$ trên đoạn $\left[ {0;6} \right]$ được cho bởi hình bên dưới. Hỏi hàm số $y = {\left[ {f\left( x \right)} \right]^2}$ có tối đa bao nhiêu cực trị

Cho hàm số \[y={{x}^{3}}-2{{x}^{2}}+\left( 1-m \right)x+m\] \[\left( 1 \right)\] . Đồ thị hàm số \[\left( 1 \right)\] cắt trục hoành tại 3 điểm phân biệt có hoành độ \[{{x}_{1}},\,\,{{x}_{2}},\,\,{{x}_{3}}\] thỏa mãn điều kiện \[x_{1}^{2}+x_{2}^{2}+x_{3}^{2}<4\]khi

Cho hàm số $y={{x}^{3}}+2m{{x}^{2}}+\left( m+3 \right)x+4\left( {{C}_{m}} \right).$ Giá trị của tham số m để đưởng thẳng $\left( d \right):y=x+4$ cắt $\left( {{C}_{m}} \right)$ tại ba điểm phân biệt $A\left( 0;4 \right),B,C$ sao cho tam giác KBC có diện tích bằng $8\sqrt{2}$ với điểm $K\left( 1;3 \right)$ là

Cho các số thực a, b, c thỏa mãn . Tìm số giao điểm của đồ thị hàm số $y={{x}^{3}}+a{{x}^{2}}+bx+c$ và trục Ox.

Cho hàm số $f\left( x \right)={{x}^{4}}-2m{{x}^{2}}+4-2{{m}^{2}}$. Có tất cả bao nhiêu số nguyên $m\in \left( -10;10 \right)$ để hàm số $y=\left| \pi f\left( x \right) \right|$ có đúng 3 cực trị.