đề ôn toán hk 2

Tính thể tích V của vật thể nằm giữa hai mặt phẳng \[x=0\] và \[x=\pi ,\] biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ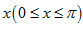  là một tam giác đều cạnh là \[2\text{ }\sqrt{sinx}\]. 

Tìm họ nguyên hàm $I=\int{\frac{9\cos x-5\sin x}{\cos x+\operatorname{s}\text{inx}}dx}.$ 

Cho hàm số \[y=f\left( x \right)\] có đạo hàm là \[f'\left( x\text{ } \right)=1\] và \[f\left( 1 \right)=1\]. Giá trị \[f\left( 5 \right)\] bằng

Cho hàm số $f\left( x \right)$ liên tục và nhận giá trị dương trên $\left[ 0;1 \right]$. Biết $f\left( x \right).f\left( 1-x \right)=1$ mọi x thuộc $\left[ 0;1 \right]$. Tính giá trị $I=\int\limits_{0}^{1}{\frac{dx}{1+f\left( x \right)}}$.

Một vật đang chuyển động với vận tốc $10\left( m/s \right)$ thì tăng tốc với gia tốc$a\left( t \right)=3t+{{t}^{2}}\left( m/{{s}^{2}} \right)$. Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc là bao nhiêu?