đề thi của ngân

Tìm nguyên hàm của hàm số $f(x)={{e}^{x}}(1+{{e}^{-x}}).$

Cho hàm số $y=f\left( x \right)$ liên tục và có đồ thị như hình bên. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đã cho và trục Ox. Quay hình phẳng D quanh trục Ox ta được khối tròn xoay có thể tích V được xác định theo công thức ?

Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ a;b \right]$. Diện tích S  của hình phẳng giới hạn bởi đồ thị của hàm số $y=f\left( x \right),$ trục hoành và hai đường thẳng $x=a,x=b\left( a

Cho parabol $\left( P \right):y={{x}^{2}}+2$ và hai tiếp tuyến của $\left( P \right)$ tại các điểm $M\left( -1;3 \right)$ và $N\left( 2;6 \right).$ Diện tích hình phẳng giới hạn bởi $\left( P \right)$ và hai tiếp tuyến đó bằng:

Biết  \[\int\limits_{0}^{\frac{\pi }{4}}{(1+x)\cos 2xdx}=\frac{1}{a}+\frac{\pi }{b}\] (với a,b là các số hữu tỉ) ,giá trị của  $a.b$ là

Một chất điểm chuyển động theo quy luật $s=12{{t}^{2}}-2{{t}^{3}}+3$ trong đó t là khoảng  thời gian (tính bằng giây) mà chất điểm bắt đầu chuyển động. Tính thời điểm t (giây) mà tại đó vận tốc (m/s) của chuyển động đạt giá trị lớn nhất.

Một chất điểm chuyển động theo quy luật \[S=\text{ }6{{t}^{2}}-{{t}^{3}}\] vận tốc \[v\left( m/s \right)\] của chuyển động đạt giá trị lớn nhất tại thời điểm $t\left( s \right)$ bằng

Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của hàm số $\left( H \right):y = \frac{{x - 1}}{{x + 1}}$ và các trục tọa độ. Khi đó giá trị của S bằng

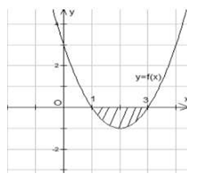
Gọi $S$ là diện tích miền hình phẳng được tô đậm trong hình vẽ dưới đây. Công thức tính $S$ là

Thể tích của khối tròn xoay thu được khi quay quanh trục Ox h̀ình phẳng giới hạn bới đồ thị hàm số $y=\sqrt{x}{{e}^{x}},$ trục hoành và đường thẳng $x=1$ là:

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ \frac{1}{3} \right\}$thỏa mãn $f'\left( x \right)=\frac{3}{3x-1},f\left( 0 \right)=1$ và $f\left( \frac{2}{3} \right)=2.$ Giá trị của biểu thức $f\left( -1 \right)+f\left( 3 \right)$ bằng:

Biết    với a, b là các số thực. Mệnh đề nào dưới đây đúng ?

Tìm nguyên hàm của hàm số $f\left( x \right)={{3}^{x}}.$

Biết $\int\limits_{1}^{e}{\frac{\left( x+1 \right)\ln x+2}{1+x\ln x}dx}=a.e+b.\ln \left( \frac{e+1}{e} \right)$ trong đó a, b là các số nguyên. Khi đó, tỷ số $\frac{a}{b}$ là:

Cho $\int\limits_{-1}^{5}{f\left( x \right)dx=4.}$ Tính $I=\int\limits_{-1}^{5}{f\left( 2x+1 \right)dx}$.

Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các đường \[y=f\left( x \right),\]trục Ox và hai đường thẳng \[x=a,x=b\] xung quanh trục Ox.

Nếu $\int{f\left( x \right)dx}=\frac{1}{x}+\ln \left| 5x \right|+C$ với  thì hàm số $f\left( x \right)$ là      

Họ nguyên hàm của hàm số $f\left( x \right)=\frac{1}{x+1}$ là

Cho $F\left( x \right)$ là một nguyên hàm của hàm số $f\left( x \right)={{x}^{2}}.$ Giá trị của biểu thức $F'\left( 4 \right)$ là:

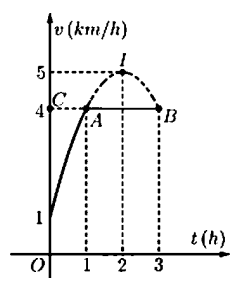
Một vật chuyển động trong 3 giờ với vận tốc  v (km/h) phụ thuộc vào thời gian t(h)

 có đồ thị vận tốc như hình bên. Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh I(2;5) và trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường mà vật di chuyển được trong 3 giờ đó.