de thi kscl toán

Một nguyên hàm của $f\left( x \right)=\left( 2x-1 \right){{e}^{\frac{1}{x}}}$ là $F\left( x \right)=\left( a{{x}^{2}}+bx+c+\frac{d}{x} \right){{e}^{\frac{1}{x}}}.$ Tính $a+b+c+d$ 

Cho hàm số $y=f\left( x \right)>0$ xác định, có đạo hàm trên đoạn $\left[ 0;1 \right]$ và thỏa mãn:

$g\left( x \right)=1+2018\int\limits_{0}^{x}{f\left( t \right)}dt,g\left( x \right)={{f}^{2}}\left( x \right).$ Tính $\int\limits_{0}^{1}{\sqrt{g\left( x \right)}d\text{x}}$ 

Cho \[\int\limits_{\ln 2}^{1+\ln 2}{f\left( x \right)dx}=2018.\] Tính \[I=\int\limits_{1}^{e}{\frac{1}{x}f\left( \ln 2x \right)dx}.\]

Cho parabol $\left( P \right)$có đồ thị như hình vẽ:

Tính diện tích giới hạn bởi $\left( P \right)$và trục hoành.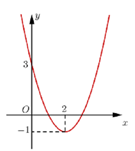

Tìm $a+b+c$ biết \[\int\limits_{e}^{{{e}^{2}}}{\frac{dx}{x\ln x\ln ex}}=a\ln 2+b\ln 3+c\].