Đề thi môn logarit ngày 3/11

Đặt \[a={{\log }_{3}}45\]. Mệnh đề nào dưới đây đúng ?

Tìm tập xác định D của hàm số $y={{e}^{{{x}^{2}}-2x}}.$

Tìm nghiệm của phương trình ${{5}^{2018x}}={{\sqrt{5}}^{2018}}.$ 

Tìm số nghiệm của phương trình ${{\log }_{5}}\left( 1+{{x}^{2}} \right)+{{\log }_{\frac{1}{3}}}\left( 1-{{x}^{2}} \right)=0$ 

Với ${{\log }_{2}}5=a,$ giá trị của \[lo{{g}_{4}}1250\] là

Tính đạo hàm của hàm số $y={{\log }_{2}}\left( 2x+1 \right).$ 

Trong các khẳng định sau, khẳng định nào sai?

Số nghiệm của phương trình: ${{\log }_{2}}x+{{\log }_{2}}\left( x-6 \right)={{\log }_{2}}7$ là:

Cho hàm số \[y=\ln \frac{1}{x+1}\]. Xác định mệnh đề đúng.

Trong các mệnh đề sau, mệnh đề nào đây sai ?

Cho biểu thức \[P=\sqrt[5]{{{x}^{3}}\sqrt[3]{{{x}^{2}}\sqrt{x}}}\]với\[x>0.\] Mệnh đề nào sau đây đúng? 

Hàm số $y=\ln \left( {{x}^{2}}+mx+1 \right)$ xác định với mọi giá trị của x khi

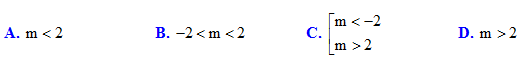
Tính giá trị của biểu thức $P=\log \left( \tan {{1}^{\circ }} \right)+\log \left( \tan {{2}^{\circ }} \right)+log\left( \tan {{3}^{\circ }} \right)+...+\log \left( \tan {{89}^{\circ }} \right).$ 

Cho $a>0,b>0$ thỏa mãn ${{a}^{2}}+9{{b}^{2}}=10ab$. Khẳng định nào sau đây đúng?

Cho hàm số $y={{\left( \frac{3}{\pi } \right)}^{{{x}^{2}}+2x+3}}.$ Tìm khẳng định đúng.

Cho các số thực a, b. Giá trị của biểu thức $A={{\log }_{2}}\frac{1}{{{2}^{a}}}+{{\log }_{2}}\frac{1}{{{2}^{b}}}$ bằng giá trị của biểu thức nào trong các biểu thức sau đây ?

Rút gọn biểu thức $P={{a}^{\frac{3}{2}}}.\sqrt[3]{a}$ với $a>0$

Bất phương trình ${{2}^{x+2}}+{{8.2}^{-x}}-33

Gọi ${{x}_{1}},{{x}_{2}}$ là hai nghiệm của phương trình ${{9}^{x+1}}-{{20.3}^{x}}+8=0.$ Khẳng định nào sau đây đúng ?

Với các số thực dương a, b bất kì. Mệnh đề nào dưới đây đúng ?