đề toán lớp 12a2

Trong không gian Oxyz, cho hai mặt phẳng \[(P):3x-y-3z+2=0\] và \[\left( Q \right):-4x+y+2z+1=0.\]Phương trình đường thẳng đi qua gốc tọa độ O và song song với 2 mặt phẳng (P) và (Q) là:

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left( P \right)$ có vecto pháp tuyến là $\overrightarrow{n}=\left( 2;-1;1 \right)$. Vectơ nào sau đây cũng là vectơ pháp tuyến của $\left( P \right)$ ?

Trong không gian Oxyz, cho mặt phẳng $\left( P \right):2x-2y+z+5=0.$ Khoảng cách từ điểm $M\left( -1;2;-3 \right)$ đến mp(P) bằng:

Cho hai mặt phẳng 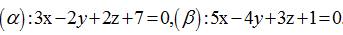 . Phương trình mặt phẳng đi qua gốc tọa độ O đồng thời vuông góc với cả  và  là:

Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng đi qua các điểm $A\left( 2;0;0 \right);B\left( 0;3;0 \right),C\left( 0;0;4 \right)$ có phương trình là:

Trong không gian Oxyz, cho 2 điểm \[B\left( 1;\text{ }2;-3 \right),\text{ }C\left( 7;\text{ }4;-2 \right)\text{ }.\] Nếu E là điểm thỏa mãn đẳng thức \[\overrightarrow{CE}=2\overrightarrow{EB}\] thì tọa độ điểm E là:

Trong không gian Oxyz, cho đường thẳng $d:\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{1}$ và mặt phẳng

. Trong các đường thẳng sau, đường thẳng nào nằm trong mặt phẳng

, đồng thời vuông góc và cắt đường d ?

Trong không gian Oxyz, cho tam giác ABC, biết $A\left( 1;-2;4 \right),B\left( 0;2;5 \right),C\left( 5;6;3 \right).$ Tọa độ trọng tâm G của tam giác ABC là:

Trong không gian với hệ trục tọa độ Oxyz , cho $\vec{a}=-\vec{i}+2\vec{j}-3\vec{k}$. Tọa độ của vectơ $\vec{a}$ là:

Trong không gian \[Oxyz,\] cho \[A\left( 1;2;0 \right),B\left( 3;-1;1 \right)\text{ }v\grave{a}\text{ }C\left( 1;1;1 \right).\] Tính diện tích S của tam giác ABC.