HH CHƯƠNG 2 ĐỀ 1

Một cái trống trường có bán kính hai đáy đều bằng 25 cm, thiết diện vuông góc với trục và cách đều hai đáy có chu vi 70$\pi $ (cm). Chiều cao của trống bằng 80 cm. Biết rằng mặt phẳng chứa trục cắt mặt xung quanh của trống là các parabol (như hình vẽ). Hỏi thể tích của trống?

Cho hình lăng trụ đứng ABC.A’B’C’ có một đáy là tam giác ABC vuông tại A; $AB=3a, BC=5a.$ Biết khối trụ có hai đáy là hai đường tròn nội tiếp hai tam giác ABC, A’B’C’ và có thể tích bằng $2\pi {{a}^{3}}.$ Chiều cao AA’ của lăng trụ bằng:

Cho hình chóp \[S.ABCD\] có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy

\[SA=a\sqrt{2}.\] Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp \[S.AB'C'D'\] là:

Tính diện tích mặt cầu ngoại tiếp một hình chóp tứ giác đều có cạnh bên bằng 2 và cạnh đáy bằng 1.

Cho hai hình vuông có cạnh đều bằng 5 được xếp lên nhau sao cho

đỉnh M của hình vuông này là tâm của hình vuông kia, đường chéo MN vuông góc

với cạnh PQ tạo thành hình phẳng (H) ( như hình vẽ bên). Tính thể tích V của

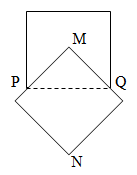
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB = BC = a và $\angle ABC={{120}^{o}}.$ Cạnh bên SA vuông góc với mặt phẳng đáy và SA = 2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.

Cho hình chóp S.ABCD có đáy là hình vuông;

                                                           \[SA\text{=}AB=a\]

 và \[SA\bot \left( ABCD \right).\] Gọi M là trung điểm AD, tính khoảng cách giữa hai đường thẳng SC và BM

Cho hình chóp S.ABCD có đáy là hình vuông, cạnh bên SA vuông góc với đáy. Gọi  M,N là trung điểm của SA,SB. Mặt phẳng MNCD chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần S.MNCD và MNABCD là:

Cho mặt cầu \[\left( S \right)\] có tâm \[I\], bán kính \[R=5\]. Một đường thẳng d cắt \[\left( S \right)\] tại hai điểm M, N phân biệt nhưng không đi qua I. Đặt \[MN=2m\] Với giá trị nào của m thì diện tích  tam giác IMN lớn nhất ?

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật $AB=a,AD=\frac{2a\sqrt{6}}{3}$, $\left( SAB \right)\bot \left( ABCD \right)$ và $SA=SB=a$. Thể tích khối cầu ngoại tiếp hình chóp $S.ABCD$ là 

Cho hàm số $f\left( x \right)={{x}^{3}}+3{{x}^{2}}+mx+1.$ Gọi S là tổng tất cả giá trị của tham số m để đồ thị hàm số $y=f\left( x \right)$ cắt đường thẳng $y=1$ tại ba điểm phân biệt $A\left( 0;1 \right), B, C$ sao cho các tiếp tuyến của đồ thị hàm số $y=f\left( x \right)$ tại B, C vuông góc với nhau. Giá trị của S bằng:

Cho hàm số$y=f\left( x \right)$ có đạo hàm là ${f}'\left( x \right)$ . Đồ thị của hàm số $y={f}'\left( x \right)$như hình vẽ bên.

Tính số điểm cực trị của hàm số $y=f\left( {{x}^{2}} \right)$trên khoảng $\left( -\sqrt{5};\sqrt{5} \right)$.

Tìm tất cả các giá trị của m để hàm số \(y=x^3-3(2m+1)x^2+(12m+5)x+2\) đồng biến trên khoảng \(\left ( 2;+\infty \right )\)

Cho hai hàm số đa thức bậc bốn $y=f(x)$ và $y=g(x)$có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số $y=f(x)$. Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là $-3$ và cắt nhau tại hai điểm nữa có hoành độ lần lượt là $-1$ và $3$. Tìm tập hợp tất cả các giá trị thực của tham số $m$ để bất phương trình $f(x)\ge g(x)+m$ nghiệm đúng với mọi $x\in \text{ }\!\![\!\!\text{ }-3;3]$.

Cho hàm số \[y=f\left( x \right)\]có đồ thị như hình vẽ bên

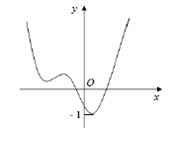
Tìm số điểm cực trị của hàm số \[y={{2}^{f\left( x \right)}}-{{3}^{f\left( x \right)}}\]

Cho hai số thực x, y thay đổi thỏa mãn điều kiện $x^{2}+y^{2}=2$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=2(x^{3}+y^{3})-3xy$. Giá trị của M + m bằng

Có bao nhiêu giá trị nguyên của tham số \[m\in [-5;5]\] để hàm số $y=\left| {{x}^{4}}+{{x}^{3}}-\frac{1}{2}{{x}^{2}}+m \right|$ có 5 điểm cực trị?

Cho hàm số $y={{x}^{3}}+2m{{x}^{2}}+\left( m+3 \right)x+4\left( {{C}_{m}} \right).$ Giá trị của tham số m để đưởng thẳng $\left( d \right):y=x+4$ cắt $\left( {{C}_{m}} \right)$ tại ba điểm phân biệt $A\left( 0;4 \right),B,C$ sao cho tam giác KBC có diện tích bằng $8\sqrt{2}$ với điểm $K\left( 1;3 \right)$ là

Cho các số thực $x,y$ thay đổi nhưng luôn thỏa mãn $3{{x}^{2}}-2xy-{{y}^{2}}=5$. Giá trị nhỏ nhất của biểu thức $P={{x}^{2}}+xy+2{{y}^{2}}$ thuộc khoảng nào sau đây?

Cho hàm số bậc ba $f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị như hình vẽ bên dưới:

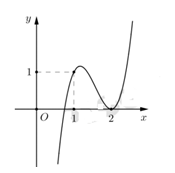
Hỏi đồ thị hàm số $g\left( x \right)=\frac{\left( {{x}^{2}}-3x+2 \right)\sqrt{x-1}}{x\left[ {{f}^{2}}\left( x \right)-f\left( x \right) \right]}$ có bao nhiêu đường tiệm cận đứng ?

Cho $f\left( x \right)=\left( {{m}^{4}}+1 \right){{x}^{4}}+\left( -{{2}^{m+1}}.{{m}^{2}}-4 \right){{x}^{2}}+{{4}^{m}}+16,m\in \mathbb{R}.$ Số cực trị của hàm số $y=\left| f\left( x \right)-1 \right|$ là:

Parabol $y=\frac{{{x}^{2}}}{2}$ chia hình tròn có tâm tại gốc tọa độ, bán kính $2\sqrt{2}$ thành 2 phần. Tỉ số diện tích của chúng thuộc khoảng nào?

Cho hàm số $f\left( x \right)$ có đồ thị hàm số $y=f'\left( x \right)$

được cho như hình vẽ bên. Hàm số $y=\left| f\left( x \right)+\frac{1}{2}{{x}^{2}}-f\left( 0 \right) \right|$

có nhiều nhất bao nhiêu điểm cực trị trong khoảng (-2;3)

Cho hàm số $f\left( x \right)={{2}^{x}}-{{2}^{-x}}$ . Gọi ${{m}_{0}}$ là số lớn nhất trong các số nguyên m thỏa mãn $f\left( m \right)+f\left( 2m-{{2}^{2}} \right)<0$ . Mệnh đề nào sau đây đúng?

Tìm tất cả các giá trị của tham số m để hàm số \[y=\frac{mx+1}{x+m}\] đồng biến trên khoảng \[(2;+\infty )\]

Cho hàm số $y=f\left( x \right)$ có hàm số $y=f'\left( x \right)$ có đồ thị hình bên. Hàm số $y=f\left( -x \right)$ đồng biến trên khoảng:

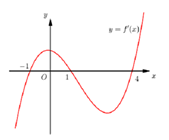
Tìm tất cả các giá trị thực của tham số m để đường thẳng $y=-2\text{x}+m$ cắt đồ thị $\left( H \right)$ của hàm số $y=\frac{2\text{x}+3}{x+2}$  tại hai điểm A, B phân biệt sao cho $P=k_{1}^{2018}+k_{2}^{2018}$ đạt giá trị nhỏ nhất (với là hệ số góc của tiếp tuyến tại A, B của đồ thị $\left( H \right)$.

Cho hàm số $y=f\left( x \right)$ liên tục và đồng biến trên $\left[ 0;\frac{\pi }{2} \right]$, bất phương trình $f\left( x \right)>\ln \left( \cos x \right)-{{e}^{\pi x}}+m$ (với m là tham số) thỏa mãn với mọi $x\in \left( 0;\frac{\pi }{2} \right)$ khi và chỉ khi:

Tìm giá trị nhỏ nhất của hàm số

Hàm số $y={{\left( x+m \right)}^{3}}+{{\left( x+n \right)}^{3}}-{{x}^{3}}$ (tham số m, n) đồng biến trên khoảng 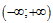Giá trị nhỏ nhất của biểu thức $P=4\left( {{m}^{2}}+{{n}^{2}} \right)-m-n$ bằng:

Cho hàm số \[y=f\left( x \right)\] xác định trên R và có đạo hàm \[y=f'\left( x \right)\] thỏa mãn

$f'\left( x \right)=\left( 1-x \right)\left( x+2 \right).g\left( x \right)+2018$ trong đó

Hàm số $y=f\left( 1-x \right)+2018x+2019$ nghịch biến trên khoảng nào ?

Cho hàm số $y=\frac{{{x}^{3}}}{3}-a{{x}^{2}}-3ax+4.$ Để hàm số đạt cực trị tại ${{x}_{1}};{{x}_{2}}$ thỏa mãn $\frac{x_{1}^{2}+2a{{x}_{2}}+9a}{{{a}^{2}}}+\frac{x_{2}^{2}+2a{{x}_{1}}+9a}{{{a}^{2}}}=2$ thì a thuộc khoảng nào ?

Xét các số thực dương x, y  thỏa mãn ${{2018}^{2({{x}^{2}}-y+1)}}=\frac{2x+y}{{{(x+1)}^{2}}}$. Tìm giá trị nhỏ nhất ${{P}_{\min }}$ của biểu thức $P=2y-3x.$ .

Có bao nhiêu giá trị nguyên của tham số m để phương trình $\cos 2x=m\sqrt{1+\tan x}.{{\cos }^{2}}x$ có nghiệm thuộc đoạn \[\text{ }\!\![\!\!\text{ 0;}\frac{\pi }{3}\text{ }\!\!]\!\!\text{ }\]?

Tìm m để đường thẳng $y=2mx+m+1$ cắt đồ thị hàm số $y=\frac{2x-1}{2x+1}$ tại hai điểm phân biệt.

Cho hàm số \[y={{x}^{3}}-2{{x}^{2}}+\left( 1-m \right)x+m\] \[\left( 1 \right)\] . Đồ thị hàm số \[\left( 1 \right)\] cắt trục hoành tại 3 điểm phân biệt có hoành độ \[{{x}_{1}},\,\,{{x}_{2}},\,\,{{x}_{3}}\] thỏa mãn điều kiện \[x_{1}^{2}+x_{2}^{2}+x_{3}^{2}<4\]khi

Cho hàm số $y=\frac{x+m}{x+1}$ (m là tham số thực) thỏa mãn $\underset{\left[ 1;2 \right]}{\mathop{\min y}}\,+\underset{\left[ 1;2 \right]}{\mathop{\max y}}\,=\frac{16}{3}$

Mệnh đề nào dưới đây đúng ?

Lập phương trình tiếp tuyến với đồ thị hàm số $y=f\left( x \right)$ thỏa mãn ${{f}^{2}}\left( 1+2x \right)=x-{{f}^{3}}\left( 1-x \right)$ tại điểm có hoành độ $x=1?$ 

Cho các số thức dương x, y thỏa mãn $2x+y=\frac{5}{4}$. Tìm giá trị nhỏ nhất ${{P}_{\min }}$ của biểu thức $P=\frac{2}{x}+\frac{1}{4y}$ 

Hình vẽ bên là đồ thị của hàm số $y=f\left( x \right).$ Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số $y=\left| f\left( x-1 \right)+m \right|$ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:

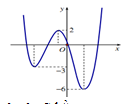
Cho hàm số $f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c$ với \[a>0\] ,\[c>2017\] và \[a+b+c

Cho hàm số \[y={{\left( x-m \right)}^{3}}-3x+{{m}^{2}}\left( {{C}_{m}} \right).\] Biết rằng điểm \[M\left( a;b \right)\] là điểm cực đại của\[\left( {{C}_{m}} \right)\] ứng với một giá trị m thích hợp đồng thời là điểm cực tiểu của \[\left( {{C}_{m}} \right)\] ứng vơi một giá trị khác của m. Tính tổng \[S=2018a+2020b\]

Cho các số thực x, y, z  thay đổi và thỏa mãn điều kiện\[{{x}^{2}}+{{y}^{2}}+{{z}^{2}}=1\]. Giá trị nhỏ nhất của biểu thức \[P={{\left( xy+yz+2xz \right)}^{2}}-\frac{8}{{{\left( x+y+z \right)}^{2}}-xy-yz+2}\]

Biết rằng đồ thị hàm số bậc 4: $y=f\left( x \right)$ được cho như hình vẽ sau:

Tìm số giao điểm của đồ thị hàm số $y=g\left( x \right)={{\left[ f'\left( x \right) \right]}^{2}}-f\left( x \right).f''\left( x \right)$ và trục Ox.

Cho đồ thị $\left( C \right):y=\frac{x}{2}+\sqrt{{{x}^{2}}+x+1}$. Gọi $M\left( 0;m \right)$ là điểm trên trục tung mà từ đó ta kẻ được ít nhất một tiếp tuyến với đồ thị $\left( C \right)$. Biết tập hợp các giá trị $m$ là nửa khoảng $\left( a;b \right]$. Giá trị của $a+b$ bằng?  

Cho hàm số $y=f\left( x \right)$ có đúng ba điểm cực trị là $-2;-1;0$ và có đạo hàm liên tục trên $\mathbb{R}.$ Khi đó hàm số $y=f\left( {{x}^{2}}-2x \right)$ có bao nhiêu điểm cực trị?

Phương trình: \[\sqrt[3]{x-1}+m\sqrt{m+1}=2\sqrt[4]{{{x}^{2}}-1}\] có nghiệm x khi: 

Cho đồ thị của ba hàm số $y=f\left( x \right),y=f'\left( x \right),y=f''\left( x \right)$ được  mô tả bằng hình vẽ. Hỏi đồ thị của các hàm số $y=f\left( x \right),y=f'\left( x \right),y=f''\left( x \right)$ theo thứ tự, lần lượt tương ứng với đường cong nào?

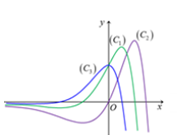
Nếu hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn $f\left( x \right)>f\left( 0 \right)\,\,\,\forall x\in \left( -1;1 \right)\backslash \left\{ 0 \right\}$ thì:

Cho hai hàm số $f\left( x \right)$ và $g\left( x \right)$ đều có đạo hàm trên $\mathbb{R}$ và thỏa mãn: ${{f}^{3}}\left( 2-x \right)-2{{f}^{2}}\left( 2+3x \right)+{{x}^{2}}.g\left( x \right)+36x=0\,\,\forall x\in \mathbb{R}$. Tính $A=3f\left( 2 \right)+4{f}'\left( 2 \right)$