hoàng khooiu nguyên

 Hàm số \[f\left( x \right)\] có đạo hàm trên \[\mathbb{R}\] là hàm số \[f'\left( x \right)\]. Biết đồ thị hàm số \[f'\left( x \right)\], hàm số \[f\left( x \right)\] nghịch biến trên khoảng: 

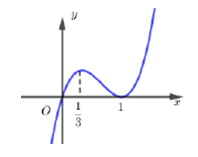
Tìm trên mỗi nhánh của đồ thị $\left( C \right):y=\frac{4x-9}{x-3}$ các điểm ${{M}_{1}},{{M}_{2}}$ để độ dài ${{M}_{1}}{{M}_{2}}$ đạt giá trị nhỏ nhất, giá trị nhỏ nhất đó bằng:

Cho tam giác ABC có \[\widehat{A}=120{}^\circ , AB=AC=a.\] Quay tam giác ABC (bao gồm cả điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng:

Cho hàm số $f\left( x \right)={{x}^{3}}-3x+1.$ Số nghiệm của phương trình ${{\left[ f\left( x \right) \right]}^{3}}-3f\left( x \right)+1=0$ là:

Gọi $M,\text{ }N$lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y={{x}^{2}}.{{e}^{-x}}$trên đoạn $\left[ -1;1 \right]$. Tính tổng $M+N$.

 Cho hàm số $y=\frac{ax+b}{x-c}$ có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau:

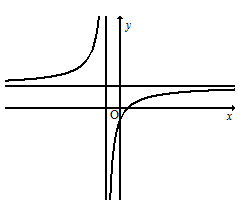
Gọi \[d\] là đường thẳng đi qua \[A\text{ }\left( 2;0 \right)\] có hệ số góc \[m\] cắt đồ thị $\left( C \right):y=-{{x}^{3}}+6{{x}^{2}}-9x+2$ tại ba điểm phân biệt \[A,\text{ }B,\text{ }C.\] Gọi \[B',\text{ }C'\] lần lượt là hình chiếu vuông góc của \[B,\text{ }C\] lên trục tung. Tìm giá trị dương của \[m\] để hình thang \[BB'C'C\]  có diện tích bằng \[8.\] 

Cho hàm số \[y=f\left( x \right)\]. Hàm số \[y=f'\left( x \right)\]có đồ thị như hình vẽ:

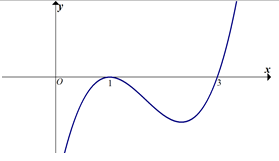
Chọn mệnh đề đúng trong các mệnh đề sau:

: Cho hàm số $y=\frac{x+m}{x+1}$ (m là tham số thực) thỏa mãn\[\underset{\left[ 0;1 \right]}{\mathop{\min }}\,\,y=3.\] Mệnh đề nào dưới đây đúng ?

Có bao nhiêu giá trị nguyên của m để hàm số \(y=x^3+(2-m)x^2-(2m-3)x+1\)đồng biến trên trên tập xác định?