Lượng giác 11

Cho phương trình $\frac{2{{\sin }^{2}}x+\cos 4x-\cos 2x}{\sin x-\cos x}=0$. Tính diện tích đa giác có đỉnh là các điểm biểu diễn góc lượng giác có số đo $\alpha $ trên đường tròn lượng giác, với $\alpha $ là nghiệm của phương trình đã cho.

Số nghiệm thuộc nửa khoảng \[\left[ -\pi ;0 \right)\] của phương trình \[\cos x-\cos 2x-\cos 3x+1=0\] là:

Tính tổng tất cả các nghiệm của phương trình \[\sin 2x+4\sin x-2\cos x-4=0\] trong đoạn \[\text{ }\!\![\!\!\text{ }0;100\pi \text{ }\!\!]\!\!\text{ }\] của phương trình

Nghiệm của phương trình $sin^{4}x+cos^{4}x+cos(x-\frac{\Pi }{4}).sin(3x-\frac{\Pi }{4})-\frac{3}{2}=0$ là

Số nghiệm của phương trình \[co{{s}^{4}}x-cos2x+2{{\sin }^{6}}x=0\] trên đoạn \[[0;2\pi ]\] là

Phương trình $\frac{c\,os4x}{c\,os2x}=\tan \,2x$ có số nghiệm thuộc khoảng $\left( 0;\frac{\pi }{2} \right)$ là:

Có bao nhiêu giá trị nguyên của tham số m để phương trình $\sqrt{1+2\cos x}+\sqrt{1+2\sin x}=\frac{m}{2}$ có nghiệm thực?

Tổng các nghiệm của phương trình \[sin\text{ }x.cos\text{ }x\text{ }+\left| sin\text{ }x+cos\text{ }x \right|=1\] trên khoảng 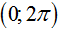là:

Tìm nghiệm của phương trình $\frac{\cos x-\sqrt{3}\operatorname{s}\text{inx}}{2\sin x-1}=0$ 

Giải phương trình $cos5x.\cos x=cos4x$. 

Số nghiệm thuộc khoảng $\left[ \frac{-4\pi }{3};\frac{\pi }{2} \right)$ của phương trình $cos\left( \pi +x \right)+\sqrt{3}s\text{inx}=\sin \left( 3x-\frac{3\pi }{2} \right)$ là:

Có bao nhiêu giá trị nguyên âm của tham số $m$ để phương trình \[m{{\sin }^{2}}x-3\sin x.\cos x-m-1=0\] có đúng 3 nghiệm \[x\in \left( 0;\frac{3\pi }{2} \right)\]?

Nghiệm của phương trình $cos2x-5\sin x-3=0$ là:

 Tính tổng S các nghiệm của phương trình \[(2\cos 2x+5)({{\sin }^{4}}x-{{\cos }^{4}}x)+3=0\] trong khoảng \[(0;2\pi ).\]

Phương trình \[\cos 2x+\cos x=0\] có bao nhiêu nghiệm thuộc khoảng  ?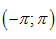

Tập hợp tất cả các giá trị của tham số m để phương trình $\left( \cos x+1 \right)\left( \cos 2x-m.\cos x \right)=m.{{\sin }^{2}}x$ có đúng hai nghiệm $x\in \left[ 0;\frac{2\pi }{3} \right]$ là $\left( a;b \right]$. Giá trị của a+b là:

Cho hàm số \[y=\frac{{{x}^{3}}}{3}+3{{x}^{2}}-2\] có đồ thị là (C). Viết phương trình tiếp tuyến với đồ thị (C) biết tiếp tuyến có hệ số góc k = -9

Tìm giá trị lớn nhất M của hàm số $y=\frac{\sin x+2\cos x+1}{\sin \text{x+}\cos x+2}.$ 

Tất cả các giá trị thực của tham số m để phương trình \[\cos 2x-\left( 2m-1 \right)\cos x-m+1=0\] có đúng 2 nghiệm thuộc đoạn \[\left[ -\frac{\pi }{2};\frac{\pi }{2} \right]\] là: 

Số giá trị nguyên của tham số m thuộc đoạn \[\left[ -2018;2018 \right]\] để phương trình $\left( m+1 \right){{\sin }^{2}}x-\sin 2x+c\text{os}2x=0$ có nghiệm là:

Trong khoảng $(-\pi; \pi)$, phương trình $sin^{6}x+3sin^{2}x.cosx+cos^{6}x=1$ có

Số nghiệm của phương trình $\frac{\sin x\sin 2x+2\sin x{{\cos }^{2}}x+\sin x+\cos x}{\sin x+\cos x}=\sqrt{3}\cos 2x$ trong khoảng \[\left( -\pi ;\pi  \right)\] là:

Tổng các nghiệm của phương trình $2\cos 3x\left( 2\cos 2x+1 \right)=1$ trên đoạn là:

Cho phương trình $m.\sin x+4\cos x=2m-5$ với m là tham số. Có bao nhiêu giá trị nguyên của m để phương trình có nghiệm ? 

Số  các giá trị nguyên của m để phương trình ${{\cos }^{2}}+\sqrt{\cos x+m}=m$ có nghiệm?

Trong các mệnh đề sau, mệnh đề nào đúng?

Tổng tất cả các nghiệm của phương trình $3\cos x-1=0$ trên đoạn 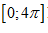 là

Tính tổng S là tổng các nghiệm thuộc đoạn \[\left[0;2\pi\right]\]của phương trình:

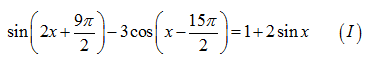
Số các giá trị thực của tham số m để phương trình $\left( \sin x-1 \right)\left( 2{{\cos }^{2}}x-\left( 2m+1 \right)\cos x+m \right)=0$ có đúng 4 nghiệm thực thuộc đoạn $\left[ 0;2\pi \right]$ là:

Phương trình ${{\sin }^{2}}x-4\sin x\cos x+3{{\cos }^{2}}x=0$ có tập nghiệm trùng với nghiệm của phương trình nào sau đây?