nguyên hàm và tích

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và có $\int\limits_{0}^{1}{f\left( x \right)d\text{x}}=2;\int\limits_{0}^{3}{f\left( x \right)d\text{x}}=6$.Tính$I=\int\limits_{-1}^{1}{f\left( \left| 2\text{x}-1 \right| \right)d\text{x}}$

Biết $\int\limits_{\frac{2\pi }{3}}^{\pi }{\frac{1-x\tan \,x}{{{x}^{2}}\cos x+x}dx=\ln \frac{\pi -a}{\pi -b}}\left( a;b\in \mathbb{Z} \right)$là. Tính $P=a+b$ ?

Cho hàm số $f\left( x \right)$ liên tục và nhận giá trị dương trên $\left[ 0;1 \right]$. Biết $f\left( x \right).f\left( 1-x \right)=1$ mọi x thuộc $\left[ 0;1 \right]$. Tính giá trị $I=\int\limits_{0}^{1}{\frac{dx}{1+f\left( x \right)}}$.

Cho hàm số $y=f\left( x \right)$ liên tục và có đạo hàm trên R thỏa mãn $f\left( 2 \right)=-2;$ $\int\limits_{0}^{2}{f\left( x \right)dx=1.}$ Tính tích phân $I=\int\limits_{0}^{4}{f'\left( \sqrt{x} \right)dx.}$

 Tích phân $\int\limits_{0}^{\pi }{\left( 3x+2 \right)c\,o{{s}^{2}}xdx}$bằng:

Cho hàm số $f\left( x \right)$ liên tục trên R và $f\left( x \right)\ne 0$ với mọi $x\in \text{R}\text{.}$ $f'\left( x \right)=\left( 2x+1 \right){{f}^{2}}\left( x \right)$ và $f\left( 1 \right)=-0,5.$ Biết rằng tổng $f\left( 1 \right)+f\left( 2 \right)+f\left( 3 \right)+...+f\left( 2017 \right)=\frac{a}{b};\,\left( a\in Z,b\in N \right)$ với $\frac{a}{b}$ tối giản. Mệnh đề nào dưới đây đúng ?

 Cho hình phẳng \[\left( H \right)\] giới hạn bởi các đường \[y={{x}^{2}},\text{ }y=0,\text{ }x=0,\text{ }x=4.\] Đường thẳng \[y=k\text{ }\left( 0

Cho miền phẳng $\left( D \right)$ giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, hai đường thẳng $x=1,\,\,x=2$ và trục hoành. Tính thể tích khối tròn xoay tạo thành khi quay $\left( D \right)$quanh trục hoành.

Biết \[\int\limits_{e}^{{{e}^{4}}}{f\left( \ln x \right)\frac{1}{x}dx}=4\]. Tính tích phân \[I=\int\limits_{1}^{4}{f\left( x \right)dx}\]

Cho $\int\limits_{0}^{3}{\frac{x}{4+2\sqrt{x+1}}dx=\frac{a}{3}}+b\ln 2+c\ln 3$, với $a,b,c\in \mathbb{Z}$. Giá trị của $a+b+c$ bằng :

Cho $f\left( x \right)$ liên tục trên $\mathbb{R}$ và $f\left( 2 \right)=16,\int\limits_{0}^{1}{f\left( 2x \right)dx=2.}$ Tích phân $\int\limits_{0}^{2}{xf'\left( x \right)dx}$ bằng:

Cho \[\int\limits_{0}^{1}{f\left( x \right)dx}=2018.\] Tích phân \[\int\limits_{0}^{\frac{\pi }{4}}{f\left( \sin 2x \right)\cos 2xdx}\] bằng

Hàm số $f\left( x \right)\frac{7\cos x-4\operatorname{s}\text{inx}}{\cos x+\operatorname{s}\text{inx}}$ có một nguyên hàm $F\left( x \right)$ thỏa mãn $F\left( \frac{\pi }{4} \right)=\frac{3\pi }{8}.$ Giá trị của $F\left( \frac{\pi }{2} \right)$ bằng:

Một vật đang chuyển động với vận tốc $10\left( m/s \right)$ thì tăng tốc với gia tốc$a\left( t \right)=3t+{{t}^{2}}\left( m/{{s}^{2}} \right)$. Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc là bao nhiêu?

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và $f\left( x \right)+2f\left( \frac{1}{x} \right)=3x.$ Tính tích phân $I=\int\limits_{\frac{1}{2}}^{2}{\frac{f\left( x \right)}{x}dx.}$ 

Thể tích $V$của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi đường tròn $(C):{{x}^{2}}+{{(y-3)}^{2}}=1$ xung quanh trục hoành là

Cho hàm số $f\left( x \right)=\frac{1}{2x+3}$ . Gọi$F\left( x \right)$ là một nguyên hàm của $f\left( x \right)$. Khẳng định nào sau đây là sai?

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -1 \right\}$ thỏa mãn ${f}'\left( x \right)=\frac{3}{x+1};$ $f\left( 0 \right)=1$và $f\left( 1 \right)+f\left( -2 \right)=2$. Giá trị $f\left( -3 \right)$ bằng

Cho hàm số \[y=f\left( x \right)\] liên tục trên \[\left[ 1;4 \right]\] và thoả mãn \[f\left( x \right)=\frac{f\left( 2\sqrt{x}-1 \right)}{\sqrt{x}}+\frac{\ln x}{x}\]. Tính tích phân \[I=\int\limits_{3}^{4}{f\left( x \right)dx}\].

Cho hàm số $f\left( x \right)$ có đạo hàm xác định, liên tục \[[0;1]\] đồng thời thỏa mãn các điều kiện $f\left( 0 \right)=-1$ và ${{\left[ f'\left( x \right) \right]}^{2}}=f''\left( x \right).$ Đặt $T=f\left( 1 \right)-f\left( 0 \right)$ hãy chọn khẳng định đúng?

Tính giá trị của tích phân \[I=\int\limits_{0}^{2}{f\left( x \right)}dx,\] biết \[f\left( x \right)=\min \left\{ 1;{{x}^{2}} \right\}.\]

Một vật chuyển động với vận tốc \[10m/s\] thì tăng tốc với gia tốc được tính theo thời gian là \[a\left( t \right)={{t}^{2}}+3t\]. Tính quãng đường vật đi được trong khoảng thời gian 3 giây kể từ khi vật bắt đầu tăng tốc.

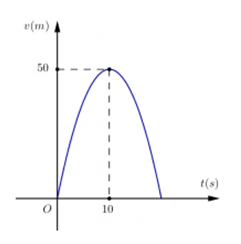
Một xe ôtô sau khi chờ đến hết đèn đỏ đã bắt đầu phóng nhanh với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường cong parabol có hình bên. Biết rằng sau 10 s thì xe đạt đến vận tốc cao nhất 50 m/s và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu đến lúc đạt vận tốc cao nhất thì xe đã đi được quãng đường bao nhiêu mét ?

 Biết tích phân $\int\limits_{0}^{\frac{\pi }{4}}{\frac{5\sin x+\cos x}{s\text{inx}+\cos x}dx}=a\pi +\ln b$ với a, b là các số hữu tỉ. Tính $S=a+b$.

Cho hàm số $y=f\left( x \right)$ thỏa mãn $f'\left( x \right).f\left( x \right)={{x}^{4}}+{{x}^{2}}$. Biết $f\left( 0 \right)=2$. Tính ${{f}^{2}}\left( 2 \right).$

Một vật đang chuyển động với vận tốc $10\left( m/s \right)$ thì tăng tốc với gia tốc$a\left( t \right)=3t+{{t}^{2}}\left( m/{{s}^{2}} \right)$. Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc là bao nhiêu?

Một nguyên hàm của $f\left( x \right)=\left( 2x-1 \right){{e}^{\frac{1}{x}}}$ là $F\left( x \right)=\left( a{{x}^{2}}+bx+c+\frac{d}{x} \right){{e}^{\frac{1}{x}}}.$ Tính $a+b+c+d$ 

Cho hàm số $f\left( x \right)$ thỏa mãn ${{\left( f'\left( x \right) \right)}^{2}}+f\left( x \right).f''\left( x \right)=15{{x}^{4}}+12x,\forall x\in \mathbb{R}$ và $f\left( 0 \right)=f'\left( 0 \right)$. Giá trị của ${{f}^{2}}\left( 1 \right)$ bằng:

Cho biết\[\int\limits_{0}^{4}{\frac{\sqrt{2x+1}}{1+\sqrt{2x+1}}dx}=a+b\ln 2,\,\left( a,b\in \mathbb{Q} \right)\]. Khi đó đẳng thức nào sau đây đúng?

Cho tích phân \[\int\limits_{\frac{\pi }{2}}^{\pi }{\frac{\cos 2x}{1-\cos x}dx}=a\pi +b\] với \[a,b\in Q.\] Tính \[P=1-{{a}^{3}}-{{b}^{2}}.\]

Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc $v\left( t \right)=7t\left( m/s \right).$ Đi được $5\left( s \right)$ người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \[a=-35\text{ }\left( m/{{s}^{2}} \right).\] Tính quãng đường của ô tô đi được tính từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn.

 Một đoàn tàu chuyển động thẳng khởi hành từ một nhà ga. Quãng đường (theo đơn vị mét $\left( m \right)$ đi được của đoàn tàu là một hàm số của thời gian $t$ (theo đơn vị giây $\left( s \right)$) cho bởi phương trình là $s=6{{t}^{2}}-{{t}^{3}}.$ Tìm thời điểm $t$ mà tại đó vận tốc $v\left( \text{m/s} \right)$ của đoàn tàu đạt giá trị lớn nhất ?

Cho số thực $a>0$. Giả  sử hàm số $f\left( x \right)$ liên tục và luôn dương trên đoạn $\left[ 0;a \right]$ thỏa mãn $f\left( x \right).f\left( a-x \right)=1,\,\,\forall x\in \left[ 0;a \right].$ Tính tích phân $I=\int\limits_{0}^{a}{\frac{1}{1+f\left( x \right)}dx}.$

 Cho hàm số \[y=f\left( x \right)\] xác định trên \[\mathbb{R}\], thỏa mãn \[f\left( x \right)>0,\text{ }\forall x\in \mathbb{R}\] và \[f'\left( x \right)+2f\left( x \right)=0\]. Tính \[f\left( -1 \right)\], biết rằng \[f\left( 1 \right)=1\].

Xét hàm số $f\left( x \right)$ liên tục trên đoạn $\left[ 0;1 \right]$ và thỏa mãn $2f\left( x \right)+3f\left( 1-x \right)=\sqrt{1-x}.$ Tích phân $\int\limits_{0}^{1}{f\left( x \right)dx}$ bằng:

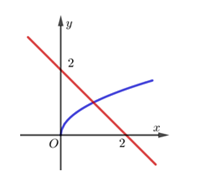
Cho hình phẳng giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, đường thẳng $y=2-x$ và trục hoành. Thể tích của khối tròn xoay sinh bởi hình phẳng trên khi quay quanh trục Ox bằng:

Cho số dương a và hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn $f\left( x \right)+f\left( -x \right)=a\,\,\forall x\in \mathbb{R}$. Giá trị của biểu thức $\int\limits_{-a}^{a}{f\left( x \right)dx}$ bằng:

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ 0;1 \right\}$ thỏa mãn ${f}'\left( x \right)=\frac{1}{x\left( x-1 \right)}$, $f\left( -1 \right)+f\left( 2 \right)=0$ và $f\left( \frac{1}{2} \right)=2$. Giá trị biểu thức $f\left( -2 \right)+f\left( \frac{1}{4} \right)+f\left( 3 \right)$ bằng:

Cho hàm số $f\left( x \right)=4{{x}^{3}}+2x+1$. Tìm $\int{f\left( x \right)dx}$.  

Cho hàm số $y=f\left( x \right)$ liên tục trên 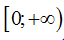 và $\int\limits_{0}^{{{x}^{2}}}{f\left( t \right)dt=x\sin x\left( \pi x \right)}.$ Tính $f\left( 4 \right)$.