PT mũ - Logarit

Giá trị của biểu thức $A={{8}^{{{\log }_{2}}3}}+{{9}^{\frac{1}{{{\log }_{2}}3}}}$ bằng:

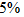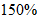Một người gửi tiết kiệm với lãi suất  một năm và lãi hàng năm được nhập vào vốn. Sau ít nhất bao nhiêu năm người đó nhận được số tiền lớn hơn số tiền gửi ban đầu ?

Tìm tập nghiệm của bất phương trình ${{\log }_{\frac{1}{2}}}\left[ {{\log }_{2}}\left( \frac{4x+1}{x-1} \right) \right]

Giải bất phương trình \[{{\log }_{3}}\left( x-1 \right)>2\]

Với giá trị nào của m phương trình \[{{4}^{x+1}}-{{2}^{x+2}}+m=0\] có nghiệm?

Tập xác định của hàm số là \[y={{\log }_{3}}\left( 4-x \right)\]

Đặt \[a={{\log }_{12}}6,b={{\log }_{2}}7\]. Hãy biểu diễn \[{{\log }_{2}}7\] theo a và b.

Hàm số \[y=\ln \left( {{x}^{2}}-2mx+4 \right)\]có tập xác định \[D=\mathbb{R}\] khi các giá trị của tham số m là:

Tập nghiệm của bất phương trình \[{{3}^{2x-1}}>27\] là:

Tính đạo hàm của hàm số \[f\left( x \right)={{\log }_{2}}\left( x+1 \right)\].

Rút gọn biểu thức $H=\frac{\sqrt{a}\sqrt[3]{a}}{\sqrt[6]{{{a}^{-7}}}}$ với a là số thực dương.

Vào 4 năm trước, chị Thương có gửi vào ngân hàng một số tiền là 20 triệu đồng theo hình thức lãi kép có kỳ hạn. Số tiền hiện tại chị nhận được là 29,186792 triệu đồng. Biết rằng, lãi suất ngân hàng tại thời điểm mà chị Thương gửi tiền là 0,8 %/tháng. Hỏi kỳ hạn $k$ mà chị Thương đã chọn là bao nhiêu tháng ?

Tìm tập nghiệm và bất phương trình ${{\left( \frac{3}{4} \right)}^{x-1}}>{{\left( \frac{3}{4} \right)}^{-x+3}}$ .

Tính đạo hàm của hàm số \[y=\text{ }lo{{g}_{2}}\left( x+{{e}^{x}} \right)\] .

Cho 4 số thực a, b, x, y với a, b là các số dương và khác 1. Mệnh đề nào dưới đây đúng?

Đặt \[a=\text{ }lo{{g}_{2}}3,\text{ }b=\text{ }lo{{g}_{5}}3.\] Nếu biểu diễn ${{\log }_{6}}45=\frac{a(m+nb)}{b(a+p)}$ thì m + n + p bằng:

Gọi a là một nghiệm của phương trình ${{4.2}^{2\log x}}-{{6}^{\log x}}-{{18.3}^{2\log x}}=0.$ Khẳng định nào sau đây đúng khi đánh giá về a ?

Giá trị lớn nhất của hàm số \[f\left( x \right)\text{ }=\text{ }\left( 2x-\text{ }3 \right){{e}^{x}}\] trên đoạn [0;3] là:

Cho a, b là hai số thực khác 0.  Biết ${{\left( \frac{1}{125} \right)}^{{{a}^{2}}+4ab}}={{\left( \sqrt[3]{625} \right)}^{3{{a}^{2}}-10ab}}.$ Tính tỉ số $\frac{a}{b}$

Cho \[0

Tìm mệnh đề đúng trong các mệnh đề sau

Nghiệm của phương trình ${{25}^{x}}-2\left( 3-x \right){{5}^{x}}+2x-7=0$ nằm trong khoảng nào sau đây?

Tập xác định của hàm số $y=\sqrt{2-\ln \left( \text{ex} \right)}$ là:

Tập xác định của hàm số \[y=\log \left( {{x}^{2}}+2x \right)\] là: 

Cho hàm số$y={{\log }_{2}}x$. Khi đó\[~xy'\] bằng: