Thi cuối học kì 1

Phương trình $\sqrt{3}\operatorname{s}\text{inx}-\cos x=1$ tương đương với phương trình nào sau đây ?

Tập giá trị của hàm số $y=t\text{anx}$ là:

Phương trình \[cos\text{x}.cos7x=cos3\text{x}.cos5x\] tương đương với phương trình nào sau đây

Phương trình \[cos2x+4\sin x+5=0\] có bao nhiêu nghiệm trên khoảng ?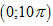 

Gọi S là tổng các nghiệm trong khoảng \[(0;\pi )\] của phương trình $\sin 2x=\frac{1}{2}.$ Tính S.

Số nghiệm nằm trong đoạn \[\left[ -\frac{\pi }{2};\frac{\pi }{2} \right]\] của phương trình  \[\sin 5x+\sin 3x=\sin 4x\]  là:

Giải phương trình $\sin 2x-{{\cos }^{4}}\frac{x}{2}-{{\sin }^{4}}\frac{x}{2}$.

Phương trình \[sin\text{x+}\sqrt{3}\cos x=1\] có tập nghiệm là:

Phương trình \[\tan x=\sqrt{3}\] có tập nghiệm là:

Tập xác định của hàm số $y=-t\text{anx}$ là:

Tìm hệ số của số hạng chứa ${{x}^{9}}$ trong khai triển nhị thức Newton $\left( 1+2x \right){{\left( 3+x \right)}^{11}}.$

 Trong kho đèn trang trí đang còn 5 bóng đèn loại I, 7 bóng đèn loại II, các bóng đèn đều khác nhau về màu sắc và hình dáng. Lấy ra 5 bóng đèn bất kỳ. Hỏi có bao nhiêu khả năng xảy ra số bóng đèn loại I nhiều hơn số bóng đèn loại II ?

Mệnh đề nào đúng trong các mệnh đề sau:

Lấy ngẫu nhiên hai viên bi từ một thùng gồm \[4\] bi xanh, \[5\] bi đỏ và $6$ bi vàng. Tính xác suất để lấy được hai viên bi khác màu ?

Lớp 11B có 25 đoàn viên trong đó 10 nam và 15 nữ. Chọn ngẫu nhiên 3 đoàn viên trong lớp để tham dự hội trại ngày 26 tháng 3. Tính xác suất để 3 đoàn viên được chọn có 2 nam và 1 nữ            

Tính số cách xếp 5 quyển sách Toán, 4 quyển sách Lý và 3 quyển sách Hóa lên một giá sách theo từng môn.

Tính số cách rút ra đồng thời hai con bài từ cỗ bài tú lơ khơ 52 con.

Từ các chữ số\[0,1,2,3,4,5,6\] có thể lập được bao nhiêu số tự nhiên chẵn có ba chữ số?

Một lô hàng có 20 sản phẩm, trong đó có 4 phế phẩm. Lấy tùy ý 6 sản phẩm từ lô hàng đó. Hãy tính xác suất để trong 6 sản phẩm lấy ra có không quá 1 phế phẩm.

Biết rằng hệ số của ${{x}^{n-2}}$ trong khai triển $\left( x-{{\frac{1}{4}}^{n}} \right)$ bằng $31$. Tìm n .

Trong mặt phẳng \[Oxy\], tìm phương tình đường tròn $\left( C' \right)$ là ảnh của đường tròn \[\left( C \right):{{x}^{2}}+{{y}^{2}}=1\] qua phép đối xứng tâm $I\left( 1;0 \right)$.

Cho \[\overrightarrow{v}\left( 3;3 \right)\] và đường tròn \[\left( C \right):{{x}^{2}}+{{y}^{2}}-2x+4y-4=0.\]. Ảnh của (C) qua \[{{T}_{\overrightarrow{v}}}\] là \[\left( C' \right):\]

Cho phép vị tự tâm O biến điểm A thành điểm B sao cho $OA=2OB.$ Khi đó tỉ số vị tự là:

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình ${{\left( x-1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=4.$ Phép vị tự tâm O (với O là gốc tọa độ) tỉ số \[k=2\] biến (C) thành đường tròn nào trong các đường tròn có phương trình sau ?

Trong mặt phẳng tọa độ $Oxy$ cho đường tròn $\left( C \right)$ có phương trình ${{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=4.$ Hỏi phép vị tự tâm $O$ tỉ số $-2$ biến đường tròn $\left( C \right)$ thành đường tròn nào sau đây ?

Trong mặt phẳng tọa độ Oxy, cho đường thẳng $d:3x-y+2=0.$ Viết phương trình đường thẳng d’ là ảnh của d qua phép quay tâm O góc quay $-{{90}^{0}}.

Cho hình bình hành ABCD, ABCD không là hình thoi. Trên đường chéo BD lấy 2 điểm M, N sao cho \[BM=MN=ND.\] Gọi P, Q là giao điểm của AN và CD; CM và AB. Tìm mệnh đề sai

Trong mặt phẳng với hệ tọa độ Oxy, cho vectơ \[\overrightarrow{v}=\left( 2;-1 \right)\] và điểm \[M\left( -3;2 \right).\] Tìm tọa độ ảnh M' của điểm M qua phép tịnh tiến theo vectơ \[\overrightarrow{v}\].

Tìm ảnh của đường tròn $(C):{{\left( x+2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=4$ qua phép tịnh tiến theo vectơ $\overrightarrow{v}\left( 1;2 \right)$ .

Cho hình chóp đều \[S.ABCD.\] Gọi O là giao điểm của AC và BD. Phát biểu nào dưới đây là đúng ?

Khẳng định nào sau đây đúng ?

Trong các khẳng định sau khẳng định nào đúng ?

Trong các mệnh đều sau, mệnh đề nào sai ?

Trong không gian, tìm mệnh đề sai trong các mệnh đề sau:

Trong các mệnh đề sau, mệnh đề nào đúng ?