Thư Dương -

Đồ thị hàm số nào sau đây cắt trục hoành tại điểm có hoành độ âm.

Tìm tất cả các giá trị của tham số $y=2{{x}^{3}}+9a{{x}^{2}}+12{{a}^{2}}x+1$ để hàm số $y=2{{x}^{3}}+9a{{x}^{2}}+12{{a}^{2}}x+1$ có cực đại, cực tiểu và hoành độ điểm cực tiểu của đồ thị hàm số bằng 1.

Đồ thị hàm số dưới đây có tiệm cận đứng ?

Cho đồ thị (C): $y=\frac{x}{x-1}$. Tìm điều kiện của m để đường thẳng d: y = -x + m cắt (C) tại hai điểm phân biệt.

Cho các chất có công thức cấu tạo sau đây: (1) CH3CH2COOCH3; (2) CH3OOCCH3; (3) HCOOC2H5; (4) CH3COOH; (5) CH3CH2COOCH3; (6) HOOCCH2CH2OH; (7) CH3OOC-COOC2H5.

Những chất thuộc loại este là

Cho m gam tinh bột lên men thành ancol etylic với hiệu suất phản ứng 81%, toàn bộ lượng CO2 hấp thụ vào dung dịch nước vôi trong thu được 375 gam kết tủa và dung dịch Y. Đun kĩ dung dịch Y thêm 150 gam kết tủa nữa. Khối lượng m là

Cho dãy các chất: phenyl axetat, anlyl axetat, etyl fomat, tripanmitin. Số chất trong dãy khi thủy phân trong dung dịch NaOH (dư), đun nóng sinh ra ancol là

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng ?

Giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y=x-\ln x$ trên đoạn $\left[ \frac{1}{2};e \right]$ lần lượt là

Cho hàm số $y={{x}^{4}}-2{{x}^{2}}+3x+2.$ Mệnh đề nào dưới đây đúng ?

Hòa tan m gam hỗn hợp X gồm Al và Na có tỉ lệ mol 1 : 2 vào nước dư thu được 4,48 lít khí (đktc). Giá trị của m là

Cho hàm số $y={{x}^{4}}-3{{x}^{2}}-2.$ Tìm số thực dương m để đường thẳng $y=m$ cắt đồ thị hàm số tại 2 điểm phân biệt A, B sao cho tam giác OAB vuông tại O, trong đó O là gốc tọa độ.

Tìm \[m\] để phương trình $2{{\sin }^{2}}x+m.\sin \,2x=2m$ vô nghiệm.

Cho hàm số $y=f\left( x \right)$ có bảng thiến thiên như sau:

Hàm số đạt cực tiểu tại điểm nào?

Đồ thị hàm số $y=\frac{\sqrt{6-{{x}^{2}}}}{{{x}^{2}}+3x-4}$ có tất cả bao nhiêu đường tiệm cận ?

Đồ thị sau đây là của hàm số nào ?

Hàm số nào sau đây không có cực trị ?

Cho hàm số $y=\frac{x+3}{x+2}.$ Khẳng định nào sau đây đúng ?

Sắp xếp các hợp chất sau đây theo thứ tự giảm dần tính bazơ:

(1) C6H5NH2;                        (2) C2H5NH2;                        (3) (C6H5)2NH;

(4) (C2H5)2NH;                     (5) NaOH;                              (6) NH3.

Tìm tập hợp S tất cả các giá trị của tham số thực m để hàm số \[y=\frac{{{x}^{3}}}{3}+m{{x}^{2}}+\left( 2m+3 \right)x+1\] đồng biến trên R.

Giá trị lớn nhất của hàm số $y={{\left( 2-x \right)}^{2}}{{e}^{x}}$ trên đoạn $\left[ 1;3 \right]$ là:

Trong số đồ thị của các hàm số $y=\frac{1}{x};y={{x}^{2}}+1;y=\frac{{{x}^{2}}+3x+7}{x-1};y=\frac{x}{{{x}^{2}}-1}$ có tất cả bao nhiêu đồ thị có tiệm cận ngang?

Cho 0,3 mol axit X đơn chức trộn với 0,25 mol ancol etylic đem thực hiện phản ứng este hóa thu được 18 gam este. Tách lấy lượng ancol và axit dư cho tác dụng với Na thấy thoát ra 2,128 lít H2. Vậy công thức của axit và hiệu suất phản ứng este hóa là

Cho hàm số có bảng biến thiên:

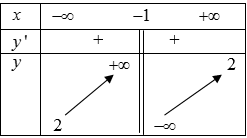
Xét các mệnh đề:

(1) \[c=1\]

(2) \[c=2\]

(3) Hàm số đồng biến trên \[\left(-\infty ;-1\right)\cup \left(-1;+\infty\right)\]

 (4) Nếu \[y'=\frac{1}{{{\left( x+1 \right)}^{2}}}\]thì \[b=1\]

Tìm số mệnh đề đúng trong các mệnh đề trên.

Tập hợp tất cả các giá trị thực của tham số m để hàm số \[y=\frac{mx-3}{2x-m}\] đồng biến trên cùng khoảng xác định là:

Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số \[y=\frac{\sqrt{1-x}-2{{x}^{2}}}{\sqrt{x}+1}.\] Khi đó giá trị của \[M-m\] là:

Gọi ${{y}_{CD}},{{y}_{CT}}$ lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số $y=\frac{{{x}^{2}}+3x+3}{x+2}$. Gía trị của biểu thức $y_{CD}^{2}-2y_{CT}^{2}$ bằng

Giá trị nhỏ nhất của hàm số \[f\left( x \right)=\frac{x-{{m}^{2}}-m}{x+1}\] trên đoạn \[\left[ 0;1 \right]\] bằng \[-2\] khi

Hàm số $y=f\left( x \right)$ có giới hạn $\underset{x\to {{a}^{-}}}{\mathop{\text{lim}}}\,\text{f}\left( x \right)=+\infty $ và đồ thị $\left( C \right)$ của hàm số $y=f\left( x \right)$ chỉ nhận đường thẳng d làm tiệm cận đứng. Khẳng định nào sau đây đúng?

Tìm giá trị lớn nhất của hàm số $y={{x}^{3}}+3{{x}^{2}}-9x+7$ trên đoạn $\left[ -2;2 \right]$.