TOÁN 12 ABC
Cho hàm số \[y=f\left( x \right)\] đạo hàm $f'\left( x \right)=-{{x}^{2}}-1.$ Với các số thực dương a, b thỏa mãn $a
Tìm tất cả các giá trị thưcj của m để hàm số \[y=\frac{mx+4}{x+m}\]nghịch biến trên khoảng (-∞;1)
Cho hàm số $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ
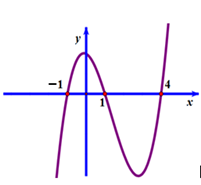 Hàm số $y=f\left( 3-2x \right)+2018$ nghịch biến trên khoảng
Hàm số $y=f\left( 3-2x \right)+2018$ nghịch biến trên khoảng
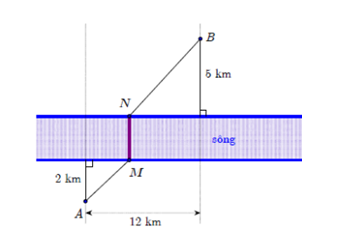
Hai thành phố A và B ngăn cách nhau bởi một còn sông. Người ta cần xây cây cầu bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố A cách bờ sông 2 km, thành phố B cách bờ sông 5 km, khoảng cách giữa đường thẳng đi qua A và đường thẳng đi qua B cùng vuông góc với bờ sông là 12 km. Giả sử hai bờ sông là hai đường thẳng song song với nhau. Nhằm tiết kiệm chi phí đi từ thành phố A đến thành phố B, người ta xây cây cầu ở vị trí MN để quãng đường đi từ thành phố A đến thành phố B là ngắn nhất (hình vẽ). Khi đó, độ dài đoạn AM là
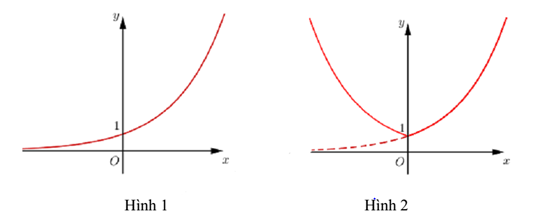
Cho hàm số$y={{\left( \sqrt{2} \right)}^{x}}$có đồ thị là hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?
Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)={{x}^{2}}\left( x-1 \right){{\left( 13x-15 \right)}^{3}}$. Khi đó số cực trị của hàm số $y=f\left( \frac{5x}{{{x}^{2}}+4} \right)$ là:
Hàm số $y=\frac{1}{3}{{x}^{3}}-2{{x}^{2}}+3x-1$ đồng biến trên khoảng
Tìm giá trị lớn nhất của hàm số $f\left( x \right)=2{{x}^{3}}+3{{x}^{2}}-12x+2$ trên đoạn $\left[ -1;2 \right]$.
Nghiệm của bất phương trình .png) là
là
Biết rằng hàm số có đồ thị được cho như hình vẽ bên. Tìm số điểm cực trị của hàm số $y=f\left[ f\left( x \right) \right]?$
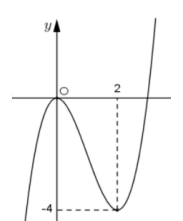
.png)
Cho hàm số $y=f\left( x \right)$ có đồ thị hàm số $y=f'\left( x \right)$ như hình vẽ. Xét hàm số $g\left( x \right)=2f\left( x \right)+2{{x}^{3}}-4x-3m-6\sqrt{5}$ với m là số thực. Để $g\left( x \right)\le 0,\forall x\in \left[ -\sqrt{5};\sqrt{5} \right]$ thì điều kiện của m là:
Cho hàm số \[y=f\left( x \right)\]. Hàm số \[y=f'\left( x \right)\]có đồ thị như hình vẽ:
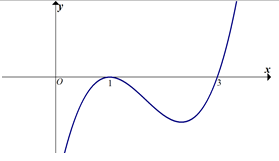
Chọn mệnh đề đúng trong các mệnh đề sau:
Cho các số thực dương x, y thỏa mãn ${{\log }_{x+y}}\left( {{x}^{2}}+{{y}^{2}} \right)\le 1.$
Giá trị lớn nhất của biểu thức $A=48{{\left( x+y \right)}^{3}}-156{{\left( x+y \right)}^{2}}+133\left( x+y \right)+4$ là
Trong không gian với hệ tọa độ Oxyz, cho điểm $A\left( 1;0;-1 \right)$ và mặt phẳng $\left( P \right):x+y-z-3=0.$ Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng $6+\sqrt{2}.$ Phương trình mặt cầu (S) là:
Tìm tất cả các giá trị của m để phương trình ${{\sin }^{4}}x+co{{s}^{4}}x+co{{s}^{2}}4x=m$ có bốn nghiệm phân biệt thuộc đoạn $\left[ -\frac{\pi }{4};\frac{\pi }{4} \right].$
Có tất cả bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số \[y=\left| {{x}^{2}}-2x+m \right|\] trên đoạn \[\left[ -1;2 \right]\] bằng 5.
Tìm tất cả các giá trị của tham số m để hàm số \[y=\frac{mx+1}{x+{{m}^{2}}}\] có giá trị lớn nhất trên đoạn \[[2;3]\] bằng \[\frac{5}{6}.\]
Cho hàm số $f\left( x \right)$ có đạo hàm $f'\left( x \right)={{\left( x+1 \right)}^{4}}{{\left( x-2 \right)}^{5}}{{\left( x+3 \right)}^{3}}.$ Số điểm cực trị của hàm số $f\left( \left| x \right| \right)$ là:
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:
Tìm tất cả các giá trị thực của tham số m để phương trình $f\left( x \right)=m+1$ có 3 nghiệm thực phân biệt?
Cho đồ thị $\left( C \right)$ của hàm số $y=\frac{2x+2}{x-1}.$Tọa độ điểm M nằm trên $\left( C \right)$ sao cho tổng khoảng cách từ M đến hai tiệm cận của $\left( C \right)$ nhỏ nhất là:
Phương trình \[{{x}^{3}}+x\left( x+1 \right)=m{{\left( {{x}^{2}}+1 \right)}^{2}}\] có nghiệm thực khi và chỉ khi:
Cho $\left( {{C}_{m}} \right):2{{\text{x}}^{3}}-\left( 3m+3 \right){{x}^{2}}+6m\text{x}-4.$ Gọi T là tập hợp các giá trị của m thỏa mãn $\left( {{C}_{m}} \right)$ có đúng hai điểm chung với trục hoành, tính tổng S các phần tử của T.
Hàm số nào dưới đây có đồ thị như hình vẽ
: Cho hàm số $y=\frac{x+m}{x+1}$ (m là tham số thực) thỏa mãn\[\underset{\left[ 0;1 \right]}{\mathop{\min }}\,\,y=3.\] Mệnh đề nào dưới đây đúng ?
Tìm tất cả các giá trị thực của tham số m để hàm số \[y={{\sin }^{3}}x-3{{\cos }^{2}}x-m\sin x-1\] đồng biến trên đoạn \[\left[ 0;\frac{\pi }{2} \right]\].
Cho hàm số $y=f\left( x \right)$. Đồ thị của hàm số $y={{f}^{'}}\left( x \right)$ như hình bên. Đặt $h\left( x \right)=f\left( x \right)-\frac{{{x}^{2}}}{2}$. Mệnh đề nào dưới đây đúng ?
.png)
Biết giá trị lớn nhất của hàm số $f\left( x \right)=\left| {{x}^{3}}+3{{x}^{2}}-72x+90 \right|+m$ trên đoạn $\left[ -5;5 \right]$ là 2018. Trong các khẳng định dưới đây, khẳng định nào đúng?
Cho hàm số $f\left( x \right)$liên tục trong đoạn $\left[ 1;e \right]$, biết $\int\limits_{1}^{e}{\frac{f\left( x \right)}{x}dx}=1,f\left( e \right)=2.$ Tích phân $\int\limits_{1}^{e}{f'\left( x \right)\ln xdx}=?$
Cho hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng ?
.png)
Tìm
m để hàm số \[y=-x{}^{3}-m\text{x}+\frac{3}{28{{\text{x}}^{7}}}\]nghịch biến 
Tìm tất cả các giá trị của m để hàm số $y=\frac{mx+3}{x+2}$ nghịch biến trên từng khoảng xác định của nó.
Cho hàm số $y=\frac{ax-b}{bx+1}$có đồ thị $\left( C \right)$. Nếu $\left( C \right)$ có tiệm cận ngang là đường thẳng $y=2$ và tiệm cận đứng là đường thẳng $x=\frac{1}{3}$ thì các giá trị của a và b lần lượt là :
Một kỹ sư thiết một cây cột ăngten độc đáo gồm các khối cầu kim loại xếp chồng lên nhau sao cho khối cầu ở trên có bán kính bằng một nửa khối cầu ở dưới. Biết khối cầu dưới cùng có bán kính là\[R=2m.\] Hỏi cây cột ăngten có chiều cao như thế nào?
Gọi \[S=\left( -\infty ;\frac{a}{b} \right]\] (với \[\frac{a}{b}\] là phân số tối giản, \[a\in Z,b\in {{N}^{*}}\]) là tập hợp tất cả các giá trị của tham số m sao cho phương trình \[\sqrt{2{{x}^{2}}+mx+1}=x+3\] có hai nghiệm phân biệt. Tính \[B={{a}^{2}}-{{b}^{3}}.\]
Cho $(\frac{3-2x}{\sqrt{4x-1}})$'=$\frac{ax-b}{(4x-1).\sqrt{4x-1}}$, $\forall x> \frac{1}{4}$. Tính $\frac{a}{b}$.
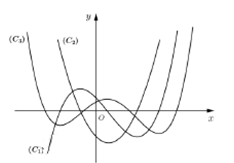
Cho hàm số \[y=f\left( x \right)\] liên tục và có đạo hàm cấp hai trên \[\mathbb{R}\]. Đồ thị của các hàm số \[y=f\left( x \right), y=f'\left( x \right)\] và \[y=f''\left( x \right)\] lần lượt là các đường cong nào trong hình vẽ bên.
Cho hàm số $y=\frac{2x-1}{x+1}$ có đồ thị $\left( C \right)$. Tìm tất cả các giá trị của tham số $m$ để đường thẳng $d:y=-x+m$ cắt đồ thị $\left( C \right)$ tại hai điểm phân biệt $A$ và $B$ đều có hoành độ âm.
Cho hàm số $y=f\left( x \right)$ có đúng ba điểm cực trị là 0; 1; 2 và có đạo hàm liên tục trên R. Khi đó hàm số $y=f\left( 4x-4{{x}^{2}} \right)$ có bao nhiêu điểm cực trị?
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y={{x}^{4}}-2m{{x}^{2}}+2m+{{m}^{4}}$ có ba điểm cực trị tạo thành một tam giác đều
Cho hàm số \[y=\frac{1}{3}{{x}^{3}}-3{{x}^{2}}+x+1\] có đồ thị (C). Trong các tiếp tuyến với đồ thị (C), hãy tìm phương trình tiếp tuyến có hệ số góc nhỏ nhất.
| 1 |
binhvipo122
Hải Trần
|
10/40
|
TOÁN 12 ABC
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm