TOÁN 12 CHƯƠNG 1

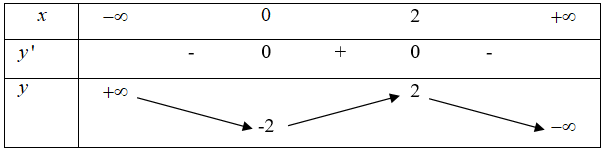
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ:

 Tìm tất cả các giá trị của tham số thực để phương trình $\left| f\left( x \right)=2-3m \right|$ có bốn nghiệm phân biệt.

Phương trình $\left| {{x}^{3}}-3x+1 \right|=m$; ($m$ là tham số) có 6 nghiệm phân biệt khi:

Cho hàm số $y={{x}^{3}}-3x+2.$ Tọa độ điểm cực tiểu của đồ thị hàm số là:

Cho hàm số $y={{x}^{4}}-6{{x}^{2}}+3$ có đồ thị là $\left( C \right)$. Parabol $P:\,y=-{{x}^{2}}-1$ cắt đồ thị $\left( C \right)$ tại bốn điểm phân biệt. Tổng bình phương các hoành độ giao điểm của $P$ và $\left( C \right)$ bằng:

Trong các hàm số sau, hàm số nào nghịch biến trên R?

Đồ thị của hàm số nào trong các hàm số sau đây có tiệm cận ngang ?

Hàm số $y={{x}^{3}}+2a{{x}^{2}}+4bx-2018\left( a,b\in \mathbb{R} \right)$ đạt cực trị tại $x=-1.$ Khi đó hiệu $a-b$ là:

2,19 gam hỗn hợp gồm Cu, Al tác dụng hoàn toàn với dung dịch HNO3 dư, thu được dung dịch Y và 0,672 lít khí NO (đktc, là sản phẩm khử duy nhất). Khối lượng muối trong Y là

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình vẽ bên. Mệnh đề nào dưới đây đúng ?

Trong các hàm số sau, hàm số nào nghịch biến trên khoảng \[\left( 0;\sqrt{2} \right)\] ?

Số đường tiệm cận của đồ thị hàm số $y=\frac{{{x}^{2}}-5x+4}{{{x}^{2}}-1}$ ? 

Tìm tất cả các giá trị thực của tham số m để phương trình ${{x}^{3}}-3x+2m=0$ có ba nghiệm thực phân biệt.

Gọi d là tiếp tuyến với đồ thị hàm số \[\left( C \right):y=\frac{1}{{{x}^{2}}-1}\] song song với trục hoành. Tìm hoành độ tiếp điểm \[{{x}_{0}}\] của d và \[\left( C \right).\]

Bảng biến thiên sau là bảng biến thiên của hàm số nào sau đây?

Thủy phân este C4H6O2 trong môi trường kiềm thu được hỗn hợp sản phẩm mà các chất sản phẩm đều có phản ứng tráng gương, cấu tạo có thể có của este là

Có bao nhiêu số nguyên m để phương trình \[5\sin x-12\cos x=m\] có nghiệm ?

Giá trị nhỏ nhất, giá trị lớn nhất của hàm số $y=x-\ln x$ trên đoạn $\left[ \frac{1}{2};e \right]$ lần lượt là

Cho hàm số

$y=f\left( x \right)$

xác định trên tập

$D=\mathbb{R}\backslash \left\{ -1 \right\}$

và liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:

Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình $f\left( x \right)=m-1$ có hai nghiệm thực phân biệt là:

Cho hàm số $f\left( x \right)={{x}^{3}}-3{{x}^{2}}+2$. Tập nghiệm của bất phương trình $f'\left( x \right)>0$ là:

Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên như sau

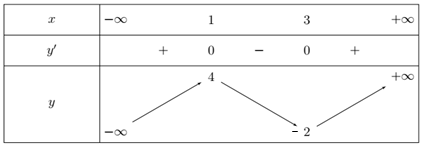
Phương trình \[f\left( x \right)-2m=0\] có 3 nghiệm khi

Để khử chua cho đất người ta thường sử dụng chất nào sau đây?

Nghiệm lớn nhất của phương trình $\sin 3x-\cos x=0$ thuộc đoạn $\left[ -\frac{\pi }{2};\frac{3\pi }{2} \right]$ là:

Kết luận nào sau đây về tính đơn điệu của hàm số \[y=\frac{2x+1}{x+1}\] là đúng ?

Hàm số \[y=\left| x \right|\] có bao nhiêu điểm cực trị ?

Hàm số nào sau đây luôn có điểm cực trị:

Tìm m để hàm số \[y=-x{}^{3}-m\text{x}+\frac{3}{28{{\text{x}}^{7}}}\]nghịch biến

Tìm điều kiện của m để đồ thị hàm số $y=\frac{x}{\sqrt{1-m{{x}^{2}}}}$ có hai tiệm cận ngang.

Cho hàm số $y=f\left( x \right)$ có $f'\left( x \right)=\frac{1}{x+1}$ . Biết rằng $f\left( 0 \right)=2018$. Giá trị của biểu thức $f\left( 3 \right)-f\left( 1 \right)$ bằng:

Cho hàm số $y=f(x)$. Hàm số $y={f}'(x)$ có đồ thị như hình bên. Hàm số $y=f\left( 3-2x \right)$ nghịch biến trên khoảng:

Có bao nhiêu giá trị nguyên của \[m\] để hàm số \[f\left( x \right)={{x}^{3}}+3{{x}^{2}}-\left( {{m}^{2}}-3m+2 \right)x+5\] đồng biến trên \[\left( \text{ }0;2\text{ } \right)\text{ }?\] 

Tìm tất cả các tham số m để hàm số $y=3\left( m-1 \right)x-\left( 2m+1 \right)\cos x$ nghịch biến trên $\mathbb{R}$

Tất cả các giá trị của $m$ để phương trình $mx-\sqrt{x-3}=m+1$ có hai nghiệm thực phân biệt.

Tìm tất cả các giá trị thực của tham số m để phương trình sau có nghiệm \[x\in \left[ 1;2 \right].\]

\[{{x}^{4}}+\frac{16}{{{x}^{4}}}+4\left( {{x}^{2}}+\frac{4}{{{x}^{2}}} \right)-12\left( x-\frac{2}{x} \right)=m.\]

Cho hàm số \[y=\frac{1}{3}{{x}^{3}}-3{{x}^{2}}+x+1\] có đồ thị (C). Trong các tiếp tuyến với đồ thị (C), hãy tìm phương trình tiếp tuyến có hệ số góc nhỏ nhất.

Tìm tất cả các giá trị của m để hàm số $y=mx^3-3mx^2+4x-1$ đồng biến trên $\mathbb{R}$.

Gọi m là số thực dương sao cho đường thẳng $y=m+1$ cắt đồ thị hàm số $y={{x}^{4}}-3{{x}^{2}}-2$ tại hai điểm A, B thỏa mãn tam giác OAB vuông tại O (O là gốc tọa độ). Kết luận nào sau đây là đúng ?

 Tìm tất cả các giá trị thực của m để hàm số \[y=\frac{\cos x-1}{\cos x-m}\] đồng biến trên khoảng \[\left( 0;\frac{\pi }{2} \right).\]

Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right)=\frac{{{x}^{2}}-3x+6}{x-1}$ trên đoạn $\left[ 2;4 \right]$ lần lượt là $M,\,\,m$. Tính $S=M+m$. 

Cho hàm số $y=\frac{x+1}{x-2}$. Số các giá trị tham số m để đường thẳng $y=m+x$ luôn cắt đồ thị hàm số tại hai điểm phân biệt A, B sao cho trọng tâm tam giác OAB nằm trên đường tròn ${{x}^{2}}+{{y}^{2}}-3y=4$ là:

 Hàm số \[f\left( x \right)\] có đạo hàm trên \[\mathbb{R}\] là hàm số \[f'\left( x \right)\]. Biết đồ thị hàm số \[f'\left( x \right)\], hàm số \[f\left( x \right)\] nghịch biến trên khoảng: 

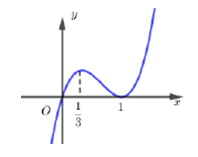
Biết đồ thị hàm số $f\left( x \right)=a\,{{x}^{3}}+b{{x}^{2}}+cx+d$ cắt trục hoành tại ba điểm phân biệt có hoành độ lần lượt là ${{x}_{1}},{{x}_{2}},{{x}_{3}}.$ Tính giá trị của biểu thức $T=\frac{1}{f'\left( {{x}_{1}} \right)}+\frac{1}{f'\left( {{x}_{2}} \right)}+\frac{1}{f'\left( {{x}_{3}} \right)}.$

Cho hàm số $y=f\left( x \right)={{x}^{3}}-6{{x}^{2}}+9x+1.$Phương trình $f\left[ f\left( f\left( x \right)-1 \right)-2 \right]=1$ có tất cả bao nhiêu nghiệm thực?

Cho hàm số $f\left( x \right)$ xác định trên tập số thực $\mathbb{R}$và có đồ thị ${f}'\left( x \right)$như hình sau

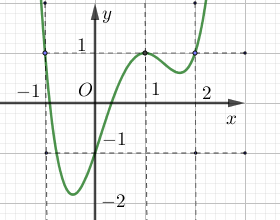
Đặt $g\left( x \right)=f\left( x \right)-x$, hàm số $g\left( x \right)$ nghịch biến trên khoảng

Cho x, y là các số thực dương thỏa mãn $2\left( {{x}^{2}}+{{y}^{2}} \right)+xy=\left( x+y \right)\left( xy+2 \right).$ Giá trị nhỏ nhất của biểu thức

Cho hàm số $f(x)$ có đạo hàm$f'(x)={{(x+1)}^{4}}{{(x-m)}^{5}}{{(x+3)}^{3}}$. Có bao nhiêu giá trị nguyên của tham số m trong đoạn$\left[ -5;5 \right]$  để số điểm cực trị của hàm số$f(\left| x \right|)$ bằng $3$:

Cho hàm số $f\left( x \right)=\left( {{a}^{2}}+1 \right){{\ln }^{2017}}\left( x+\sqrt{1+{{x}^{2}}} \right)+bx{{\sin }^{2018}}+2$ với a, b là các số thực và $f\left( {{7}^{\log 5}} \right)=6.$ Tính $f\left( -{{5}^{\log 7}} \right)$.

Có bao nhiêu giá trị nguyên của tham số m để phương trình$\sin 2x+cos2x+\left| \sin x+cosx \right|-\sqrt{co{{s}^{2}}x+m}-m=0$ có nghiệm thực?

Một màn ảnh hình chữ nhật cao 1,4m được đặt ở độ cao 1,8m so với tầm mắt (tính đầu mép dưới của màn hình). 

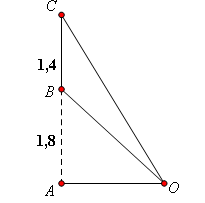
Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác định khoảng cách đó. 

Cho hàm số$y=f\left( x \right)$ có đồ thị như hình bên. Có bao nhiêu số nguyên m để phương trình $\frac{1}{3}f\left( \frac{x}{2}+1 \right)+x=m$ có nghiệm thuộc đoạn $\left[ -2;2 \right]$?

Lập phương trình tiếp tuyến với đồ thị hàm số $y=f\left( x \right)$ thỏa mãn ${{f}^{2}}\left( 1+2x \right)=x-{{f}^{3}}\left( 1-x \right)$ tại điểm có hoành độ $x=1?$