toán 12 đề 1

Giả sử a, b là các số thực sao cho ${{x}^{3}}+{{y}^{3}}=a{{.10}^{3z}}+b{{.10}^{2z}}$ đúng với mọi các số thực dương x, y, z thỏa mãn $\log \left( x+y \right)=z$ và $\log \left( {{x}^{2}}+{{y}^{2}} \right)=z+1$. Giá trị của $a+b$ bằng:

Cho hai số thực x,y thỏa mãn $0\le x\le \frac{1}{2},\,0

Gọi a là giá trị nhỏ nhất của $f(n)=\frac{({{\log }_{3}}2)({{\log }_{3}}3)({{\log }_{3}}4)...({{\log }_{3}}n)}{{{9}^{n}}}$ với \[n\in N,n\ge \text{ }2.\] Có bao nhiêu số n để f (n) = a ?

Tìm số nghiệm của phương trình ${{2}^{x}}+{{3}^{x}}+{{4}^{x}}+...+{{2017}^{x}}+{{2018}^{x}}=2017-x.$ 

Tìm bộ ba số nguyên dương (a;b;c) thỏa mãn:

log1 + log(1 + 3) + log(1 + 3 + 5) +...+ log(1 + 3 + 5 + ... + 19) − 2log5040 = a + blog2 + clog3

Tính diện tích S của hình phẳng giới hạn bởi các đường $y={{e}^{x}},\,\,y=2,\,\,x=0,\,\,x=1.$ ? 

Cho hàm số $y={{x}^{3}}-3m{{x}^{2}}+3\left( {{m}^{2}}-1 \right)x-{{m}^{3}}+4m-1$ . Đồ thị hàm số có hai điểm cực trị tạo với gốc tọa độ O một tam giác vuông tại O khi :

Phương trình ${{3.2}^{x}}+{{4.3}^{x}}+{{5.4}^{x}}={{6.5}^{x}}$ có tất cả bao nhiêu nghiệm thực?

Cho hàm số \[y=\frac{1}{3}{{x}^{3}}-3{{x}^{2}}+x+1\] có đồ thị (C). Trong các tiếp tuyến với đồ thị (C), hãy tìm phương trình tiếp tuyến có hệ số góc nhỏ nhất.

Cho hàm số $y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d,\,\,\left( a,b,c,d\in \mathbb{R} \right),$ có bảng biến thiên như hình sau:

Tìm tất cả giá trị thực của tham số $m$ để phương trình $m=\left| f\left( x \right) \right|$ có $4$ nghiệm phân biệt trong đó có đúng một nghiệm dương.

Tìm m để phương trình $\sin 2x+\sqrt{3}m=2\cos x+\sqrt{3}m\sin x$ có duy nhất một nghiệm thuộc khoảng $\left( 0;\pi \right).$

Bất phương trình $\frac{x-1}{x+1}\ge m$ có nghiệm thuộc đoạn [1; 2] khi và chỉ khi

Biết rằng các số thực a, b thay đổi sao cho hàm số $f\left( x\right)=-{{x}^{3}}+{{\left( x+a \right)}^{3}}+{{\left( x+b \right)}^{3}}$ luôn đồng biến trên khoảng\[\left( -\infty ;+\infty\right)\] . Tìm giá trị nhỏ nhất của biểu thức $P={{a}^{2}}+{{b}^{2}}-4a-4b+2.$

Tìm m để giá trị lớn nhất của hàm số $y=\left| {{x}^{2}}+2x+m-4 \right|$ trên đoạn $\left[ -2;1 \right]$ đạt giá trị nhỏ nhất. Giá trị của m là:

Có bao nhiêu giá trị nguyên của tham số m để hàm số $y=\frac{mx-8}{x-m+2}$ đồng biến trên mỗi khoảng xác định ?

Một màn ảnh hình chữ nhật cao 1,4m được đặt ở độ cao 1,8m so với tầm mắt (tính đầu mép dưới của màn hình). 

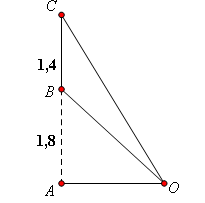
Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác định khoảng cách đó. 

Cho hàm số $f\left( x \right)$ có đồ thị hàm số $y=f'\left( x \right)$

được cho như hình vẽ bên. Hàm số $y=\left| f\left( x \right)+\frac{1}{2}{{x}^{2}}-f\left( 0 \right) \right|$

có nhiều nhất bao nhiêu điểm cực trị trong khoảng (-2;3)

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số $y=\left| 3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m \right|$ có 5 điểm cực trị?

Cho hàm số $f\left( x \right)$ có đồ thị hàm số $y=f'\left( x \right)$

được cho như hình vẽ bên. Hàm số $y=f\left( \operatorname{cosx} \right)+{{x}^{2}}-x$

đồng biến trên khoảng:

Gọi $S$ là tập các giá trị của tham số thực $m$ để hàm số $y={{x}^{2}}+\ln \left( x+m+2 \right)$ đồng biến trên tập xác định của nó. Biết $S=\left( -\infty ;a+\sqrt{b} \right]$. Tính tổng $K=a+b$ là 

Trong thời gian liên tục 25 năm, một người lao động luôn gửi đúng 4.000.000 đồng vào một ngày cố định của tháng ở ngân hàng M với lại suất không thay đổi trong suốt thời gian gửi tiền là 0,6% tháng. Gọi A là số tiền người đó có được sau 25 năm. Hỏi mệnh đề nào dưới đây là đúng ?

Một người gửi số tiền $100$ triệu đồng vào ngân hàng với lãi suất $0,5%$/tháng và ông ta rút đều đặn mỗi tháng một triệu đồng kể từ sau ngày gửi một tháng cho đến khi hết tiền (tháng cuối cùng có thể không còn đủ một triệu đồng). Hỏi ông ta rút hết tiền sau bao nhiêu tháng?

Cường độ của ánh sáng I khi đi qua môi trường khác với không khí , chẳng hạn như sương mù hay nước, ... sẽ giảm dần tùy theo độ dày của môi trường và một hằng số $\mu $gọi là khả năng hấp thu ánh sáng tùy theo bản chất môi trường mà ánh sáng truyền đi và được tính theo công thức $I={{I}_{0}}.{{e}^{-\mu x}}$ với x là độ dày của môi trường đó và tính bằng mét, ${{I}_{0}}$ là cường độ ánh sáng tại thời điểm trên mặt nước. Biết rằng nước hồ trong suốt có \[\mu =1,4\text{ }.\] Hỏi cường độ ánh sáng giảm đi bao nhiêu lần khi truyền trong hồ đó từ độ sâu $3m$ xuống đến độ sâu $30m$

( chọn giá trị gần đúng với đáp số nhất)

Cho phương trình: \[(m~-1)\log _{\frac{1}{2}}^{2}{{\left( x-2 \right)}^{2}}+4\left( m-5 \right){{\log }_{\frac{1}{2}}}\frac{1}{x-2}+4m-4=0\] (với m là tham số). Gọi \[S=~[a;b]\] là tập các giá trị của m để phương trình có nghiệm trên đoạn \[\left[ \frac{5}{2};4 \right]\]. Tính \[a+b.\]

Phương trình: \[{{\log }_{2}}\left( {{x}^{2}}-6x+7 \right)={{\log }_{2}}\left( x-3 \right)\] có tập nghiệm là:

Số nghiệm của phương trình: \[{{9}^{x}}-{{2.3}^{x+1}}+5=0\] là:

Biết ${{x}_{1}},{{x}_{2}}$ là hai nghiệm của phương trình ${{\log }_{7}}\left( \frac{4{{x}^{2}}-4x+1}{2x} \right)+4{{x}^{2}}+1=6x$ và ${{x}_{1}}+2{{x}_{2}}=\frac{1}{4}\left( a+\sqrt{b} \right)$ với a, b là hai số nguyên dương. Tính $a+b$.

Tập nghiệm của bất phương trình ${{9}^{x}}-2\left( x+5 \right){{3}^{x}}+9\left( 2x+1 \right)\ge 0$ là:

Cho x, y là các số thực dương thỏa mãn $\ln x+\ln y\ge \ln \left( {{x}^{2}}+y \right)$ là các số thực dương thỏa mãn $P=x+y$. Tính giá trị nhỏ nhất của P.