Toán cơ bản

Biết tích phân \[\int\limits_{0}^{\ln 6}{\frac{{{e}^{x}}}{1+\sqrt{{{e}^{x}}+3}}dx}=a+b\ln 2+c\ln 3\] . Tính \[T=a+b+c\].

Tích phân $\int\limits_{0}^{1}{\frac{x-1}{{{x}^{2}}-2x+2}dx}$ bằng:

Nếu F(x) là nguyên hàm của hàm số f(x) trên đoạn [a;b] thì $\int\limits_{a}^{b}{f(x)}dx$bằng

Biết $\int{x{{e}^{2x}}dx}={{e}^{2x}}+b{{e}^{2x}}+C\left( a,b\in \mathbb{Q} \right).$ Tính tích a.b.

Tìm họ nguyên hàm $F\left( x \right)=\int{\frac{1}{{{\left( 2x+1 \right)}^{3}}}\text{d}x}$.

Tìm họ nguyên hàm của hàm số $y=\frac{1}{{{\left( x+1 \right)}^{2}}}$.

Tính tích phân $I = \int\limits_1^5 {\frac{{dx}}{{x\sqrt {3x + 1} }}} $ ta được kết quả $I = a\ln 3 + b\ln 5.$

Giá trị $S = {a^2} + ab + 3{b^2}$ là

Trong hình bên, S là diện tích của hình phẳng giới hạn bởi đồ thị hàm số liên tục $y=f\left( x \right)$và đường thẳng đi qua hai điểm A(-1; -1), B(1;1). Khẳng định nào sau đây là đúng?

Nếu hàm số $y=f\left( x \right)$là một nguyên hàm của hàm số $y=\ln x$ trên $\left( 0;+\infty \right)$ thì

Đặt $\int\limits_{1}^{2}{I=\left( 2mx+1 \right)dx}$ (m là tham số thực). Tìm m để $I=4$.

Cho hàm số $y=f(x)$ liên tục trên 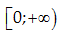và  $\int\limits_{0}^{{{x}^{2}}}{f\left( t \right)dt}=x.{{e}^{x}}$. Tính giá trị $f\left( 4 \right)$.

Cho \[{{\log }_{2}}m=a\] và \[A={{\log }_{m}}\left( 8m \right)\] với \[m > 0 ,m\ne 1.\] Tìm mối liên hệ giữa A và a.

Diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số $y=x$và $y={{e}^{x}}$, trục tung và đường thẳng $x=1$ được tính theo công thứ:

Tích phân \[I=\int\limits_{0}^{1}{\frac{{{\left( x-1 \right)}^{2}}}{{{x}^{2}}+1}\text{d}x}=a-\ln b\]. Trong đó \[a,b\] là các số nguyên. Tính giá trị của biểu thức \[a+b\].

Cho hàm số \[y=f\left( x \right)\] có đạo hàm \[f'\left( x \right)\] liên tục trên \[\left[ 0;2 \right]\] và $f\left( 2 \right)=3;\int\limits_{0}^{2}{f\left( x \right)dx=3.}$ Tính $\int\limits_{0}^{2}{x.f'\left( x \right)dx}$

Tính I=$\int\limits_{1}^{2}{xdx}$

Tích phân \[I=\int\limits_{0}^{2}{{{\left( x+2 \right)}^{3}}dx}\] bằng:

Nếu $\int\limits_{1}^{2}{f\left( x \right)dx=3,\int\limits_{2}^{5}{f\left( x \right)dx=-1}}$ thì $\int\limits_{1}^{5}{f\left( x \right)dx}$ bằng:

Cho hàm số $y=f\left( x \right)$ liên tục trên $\left[ a;b \right].$ Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số $y=f\left( x \right),$ trục hoành và hai đường thẳng $x=a,x=b$ được tình theo công thức.

 Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số $y=3\text{x}-{{x}^{2}}$ và trục hoành, quanh trục hoành.