Toánthptlýnhân12

Cho hàm số \[y={{x}^{3}}-3{{x}^{2}}\]. Tìm mệnh đề đúng.

Bảng biển thiên ở hình dưới đây là bảng biến thiên của hàm số nào ?

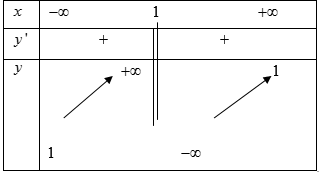
Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như hình bên dưới đây. Hỏi đồ thị hàm số $y=f\left( x \right)$ có bao nhiêu đường tiệm cận ?

Thêm từ từ từng giọt 100 ml dung dịch Na2CO3 1,2M và NaHCO3 0,6M vào dung dịch 200 ml HCl 1M. Sau phản ứng hoàn toàn thu được dung dịch X. Cho dung dịch BaCl2 dư vào dung dịch X thu được m gam kết tủa. Giá trị của m bằng

Cho hàm số $y=\frac{4}{3}{{\sin }^{3}}x+2{{\cos }^{2}}x-\left( 2{{m}^{2}}-5m+2 \right)\sin x-2017.$ Gọi S là tập hợp tất cả các giá trị nguyên của m sao cho hàm số đồng biến trên khoảng $\left( 0;\frac{\pi }{2} \right).$ Tìm số phần tử của S.

Cho hàm số \[y=f\left( x \right)\] có đồ thị như hình vẽ. Hỏi phương trình \[m=f\left( x \right)+1\] với $m<2$ có bao nhiêu nghiệm ?

Đốt cháy hoàn toàn 1 lượng hỗn hợp 2 este. Dẫn sản phẩm cháy lần lượt qua bình (1) đựng P2O5 dư và bình (2) đựng dung dịch Ca(OH)2 dư, thấy khối lượng bình (1) tăng 6,21 gam, còn bình (2) thì được 34,5 gam kết tủa. Các este trên thuộc loại este nào dưới đây?

Tìm tiệm cận ngang của đồ thị hàm số\[y=\frac{1-x}{x+2}.\]

Cho hàm số $y=\frac{mx-1}{x+m}$ (với $m$ là tham số thực) thỏa mãn $\underset{\left[ 1;4 \right]}{\mathop{\text{maxy}}}\,=1$. Mệnh đề nào dưới đây đúng ?

Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số $y\,=\,\frac{3x+4}{x+2}$ ?

Đường cong ở hình bên là đồ thị của hàm số $y=\frac{ax+b}{cx+d}$ với a, b, c, d là các số thực. Mệnh đề nào dưới đây đúng ?

Cho hàm số $y=\frac{x+1}{2-x}$. Khẳng định nào sau đây đúng:

Gọi n là số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số $y=\frac{x+1}{{{x}^{2}}-4x+3}.$ Tìm n ?

Cho hàm số \[y={{x}^{3}}+2\left( m+2 \right){{x}^{2}}+\left( 8-5m \right)x+m-5\] có đồ thị \[\left( {{C}_{m}} \right)\] và đường thẳng \[d:y=x-m+1\]. Tìm số các giá trị của m để d cắt \[\left( {{C}_{m}} \right)\] tại 3 điểm phân biệt có hoành độ tại \[{{x}_{1}},{{x}_{2}},{{x}_{3}}\] thỏa mãn \[x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=20.\].

Số tiệm cận của đồ thị hàm số \[y=\frac{x+1}{\sqrt{{{x}^{2}}-1}}\] là:

Cho hàm số $y\,=\,f(x)$ liên tục trên $\mathbb{R}$, có đạo hàm $f'(x)\,=\,{{x}^{3}}{{(x\,-\,1)}^{2}}(x\,+\,2)$. Hỏi hàm số $y\,=\,f(x)$ có bao nhiêu điểm cực trị ?

Trong công nghiệp, để sản xuất xà phòng và glixerol thì thủy phân chất nào sau đây?

Các giải thích về quan hệ cấu trúc, tính chất nào sau đây không hợp lí?

Cho hàm số $y={{x}^{3}}-3{{\text{x}}^{2}}+\left( m+1 \right)x+1$ có đồ thị $\left( {{C}_{m}} \right)$ với m là tham số. Tìm tất cả các giá trị của tham số m để đường thẳng $d:y=x+1$ cắt đồ $\left( {{C}_{m}} \right)$thị tại ba điểm phân biệt $P\left( 0;1 \right),M,N$ sao cho tam giác OMN vuông tại O (O là gốc tọa độ).

Gọi M, m theo thứ tự là giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y=\frac{{{x}^{2}}+3}{x-1}$ trên đoạn $\left[ -2;0 \right].$ Tính $P=M+m$ .

Cho hàm số \[y=f\left( x \right)\] liên tục trên \[\mathbb{R}\] và có đồ thị là đường cong như hình vẽ bên. Tìm điểm cực tiểu của đồ thị hàm số \[y=f\left( x \right)\].

Tìm số giao điểm của đồ thị hai hàm số $y=\sqrt{x+3}$ và $y=x+1.$

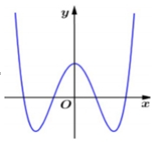
Cho hàm số $y=a{{x}^{4}}+b{{x}^{2}}+c$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là đúng? 

Cho hàm số $y=-{{x}^{3}}+3{{x}^{2}}+x-2$ có đồ thị là $\left( C \right).$ Tiếp tuyến của \[\left( C \right)\] tại giao điểm của \[\left( C \right)\] với trục tung có phương trình là:

Số điểm cực trị của hàm số $y={{x}^{4}}+100$ là:

Đồ thị hàm số nào dưới đây đi qua điểm \[M\left( 2;-1 \right)\] ? 

Số đường tiệm cận của đồ thị hàm số \[y=\frac{x-2}{{{x}^{2}}-3x-4}\] là:

Tất cả các giá trị của tham số m để hàm số \[y={{x}^{4}}-2m{{x}^{2}}+3\] có 3 cực trị là:

Tìm giá trị lớn nhất của hàm số \[y=\sqrt{x+1}+\sqrt{3-x}\] trên đoạn \[\left[ -1;3 \right]\].

Cho hàm số \[y={{x}^{4}}-2{{x}^{2}}+m-3\text{ }\left( C \right)\]. Tất cả các giá trị của m để \[\left( C \right)\] cắt trục Ox tại 4 điểm phân biệt.