Đề thi thử THPT môn Toán Chuyên ĐH Vinh lần 1 2019
Trong không gian Oxyz, cho $\overrightarrow{a}=\left( 1;-1;0 \right)$ và hai điểm $A\left( -4;7;3 \right),B\left( 4;4;5 \right)$. Giả sử M, N là hai điểm thay đổi trong mặt phẳng (Oxy) sao cho $\overrightarrow{MN}$ cùng hướng với a và $MN=5\sqrt{2}$. Giá trị lớn nhất của $\left| AM-BN \right|$ bằng:
Trong không gian Oxyz, cho ba đường thẳng Đường thẳng $d:\frac{x}{1}=\frac{y}{1}=\frac{z+1}{-2};{{\Delta }_{1}}:\frac{x-3}{2}=\frac{y}{1}=\frac{z-1}{1};{{\Delta }_{2}}:\frac{x-1}{1}=\frac{y-2}{2}=\frac{z}{1}$ . Đường thẳng $\Delta $ vuông góc với d đồng thời cắt ${{\Delta }_{1}},{{\Delta }_{2}}$ tương ứng tại H , K sao cho độ dài HK nhỏ nhất. Biết rằng $\Delta $ có một vecto chỉ phương$\overrightarrow{u}=\left( h;k;1 \right)$ .Giá trị của h-k bằng:
Cho hàm số$y=f\left( x \right)$ có đồ thị như hình bên. Có bao nhiêu số nguyên m để phương trình $\frac{1}{3}f\left( \frac{x}{2}+1 \right)+x=m$ có nghiệm thuộc đoạn $\left[ -2;2 \right]$?
.png)
Giả sử ${{z}_{1}},{{z}_{2}}$ là hai trong các số phức z thỏa mãn $\left( z-6 \right)\left( 8+\overline{zi} \right)$ là số thực. Biết rằng $\left| {{z}_{1}}-{{z}_{2}} \right|=4$. Giá trị trị nhỏ nhất của $\left| {{z}_{1}}+3{{z}_{2}} \right|$ bằng:
Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An
đã làm một chiếc mũ “cách điệu” cho Ông già Noel có hình dáng
một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên. Biết rằng OO' = 5cm, OA = 10cm, OB = 20cm, đường cong AB là một phần của một parabol có đỉnh là điểm A. Thể tích của chiếc mũ bằng
.png)
Cho hình chóp tứ giác đều S.ABCD có $SA=\sqrt{11}a$, côsin của góc hợp bởi hai mặt phẳng $\left( SBC \right)$ và $\left( SCD \right)$ bằng $\frac{1}{10}$. Thể tích của khối chóp S.ABCD bằng
Cho hàm số $f\left( x \right)$ có đồ thị hàm số $y=f'\left( x \right)$
được cho như hình vẽ bên. Hàm số $y=\left| f\left( x \right)+\frac{1}{2}{{x}^{2}}-f\left( 0 \right) \right|$
có nhiều nhất bao nhiêu điểm cực trị trong khoảng (-2;3)
.png)
Cho hàm số $f\left( x \right)$ thỏa mãn $f\left( x \right)+f'\left( x \right)={{e}^{-x}},\forall x\in \mathbb{R}$ và $f\left( 0 \right)=2$. Tất cả các nguyên hàm của $f\left( x \right){{e}^{2x}}$ là
Cho hàm số $f\left( x \right)={{2}^{x}}-{{2}^{-x}}$ . Gọi ${{m}_{0}}$ là số lớn nhất trong các số nguyên m thỏa mãn $f\left( m \right)+f\left( 2m-{{2}^{2}} \right)<0$ . Mệnh đề nào sau đây đúng?
Cho hàm số $f\left( x \right)$ có đồ thị hàm số $y=f'\left( x \right)$
được cho như hình vẽ bên. Hàm số $y=f\left( \operatorname{cosx} \right)+{{x}^{2}}-x$
đồng biến trên khoảng:
.png)
Bất phương trình $\left( {{x}^{3}}-9x \right)\ln \left( x+5 \right)\le 0$ có bao nhiêu nghiệm nguyên?
Trong không gian Oxyz, cho đường thẳng $d:\frac{x+1}{2}=\frac{y}{1}=\frac{z-2}{-1}$ và hai điểm $A\left( -1;3;1 \right),B\left( 0;2;-1 \right)$. Gọi $C\left( m;n;p \right)$ là điểm thuộc d sao cho diện tích của tam giác ABC bằng $2\sqrt{2}$. Giá trị của tổng $m+n+p$ bằng
Biết rằng $\int\limits_{0}^{1}{\frac{dx}{3x+5\sqrt{3x+1}+7}}=a\ln 2+b\ln 3+c\ln 5$ với a, b, c là các số hữu tỉ. Giá trị của $a+b+c$ bằng
Trong không gian Oxyz cho các điểm $M\left( 2;1;4 \right),N\left( 5;0;0 \right),P\left( 1;-3;1 \right)$. Gọi $I\left( a;b;c \right)$ là tâm của mặt cầu tiếp xúc với mặt phẳng (Oyz) đồng thời đi qua các điểm M ,N , P. Tìm c biết rằng $a+b+c<5$
Cho $f\left( x \right)$ mà hàm số $y=f'\left( x \right)$ có bảng biến thiên như hình bên. Tất cả các giá trị của tham số m để bất phương trình .png) có nghiệm đúng với mọi x thuộc (0;3) là
có nghiệm đúng với mọi x thuộc (0;3) là
.png)
Có bao nhiêu số phức z thỏa mãn ${{\left| z-1 \right|}^{2}}+\left| z-{{z}^{2}} \right|i+\left( z+\overline{z} \right){{i}^{2019}}=1$?
Cho hàm số $y=f\left( x \right)$có đồ thị như hình vẽ bên. Có
bao nhiêu số nguyên m để phương trình $f\left( {{x}^{3}}-3x \right)=m$ có 6
nghiệm phân biệt thuộc đoạn $\left[ -1;2 \right]?$
.png)
Cho hình lăng trụ đứng ABC. A 'B 'C ' có đáy ABC là tam giác vuông tại A. Gọi E là trung điểm của AB. Cho biết AB = 2a, BC = $\sqrt{13}$, CC’ = 4a. Khoảng cách giữa hai đường thẳng A 'B và CE bằng
Tất cả các nguyên hàm của hàm số $f\left( x \right)=\frac{x}{{{\sin }^{2}}x}$ trên khoảng $\left( 0;\pi \right)$là
Giải bóng truyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của Việt Nam nằm trong hai bảng khác nhau bằng
Cho hình lập phương ABCD. A 'B 'C 'D ' có I, J tương ứng là trung điểm của BC và BB ' . Góc giữa hai đường thẳng AC và IJ bằng
Gọi m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y=x+\frac{9}{x}$ trên đoạn $\left[ 1;4 \right]$. Giá trị của m + M bằng
Gọi ${{x}_{1}},{{x}_{2}}$ là các nghiệm phức của phương trình ${{z}^{2}}+4z+7=0$. Số phức ${{z}_{1}}\overline{{{z}_{2}}}+\overline{{{z}_{1}}}{{z}_{2}}$ bằng
Cho hình nón tròn xoay có bán kính đáy bằng 3 và diện tích xung quanh bằng $6\sqrt{3}\pi $. Góc ở đỉnh của hình nón đã cho bằng
Cho hàm số $y=f\left( x \right)$có bảng biến thiên như hình vẽ bên. Hàm số $y=2f\left( x \right)$ đạt cực đại tại
.png)
Cho hình lăng trụ tam giác đều ABC. A 'B 'C ' có AB = a, góc giữa đường thẳng A 'C và mặt phẳng (ABC) bằng 450. Thể tích của khối lăng trụ ABC. A’B 'C ' bằng
Biết rằng $\alpha ;\beta $ là các số thực thỏa mãn ${{2}^{\alpha }}\left( {{2}^{\alpha }}+{{2}^{\beta }} \right)=8\left( {{2}^{-\alpha }}+{{2}^{-\beta }} \right)$. Giá trị của $\alpha +2\beta $ bằng
Đồ thị hàm số $y=\frac{{{x}^{3}}-4x}{{{x}^{3}}-3x-2}$ có bao nhiêu đường tiệm cận?
Cho hàm số $y=f\left( x \right)$có đạo hàm $f'\left( x \right)={{x}^{2}}\left( {{x}^{2}}-1 \right),\forall x\in \mathbb{R}.$ Hàm số $y=2f\left( -x \right)$ đồng biến trên khoảng
Cho $f\left( x \right)={{x}^{4}}-5{{x}^{2}}+4$. Gọi S là diện tích của hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right)$ và trục hoành.. Mệnh đề nào sau đây sai?
Đạo hàm của hàm số $f\left( x \right)=\frac{{{3}^{x}}-1}{{{3}^{x}}+1}$ là
Biết rằng phương trình $\log _{2}^{2}x-7{{\log }_{2}}x+9=0$ có hai nghiệm ${{x}_{1}},{{x}_{2}}$. Giá trị ${{x}_{1}}{{x}_{2}}$ bằng:
Cho hình trụ tròn xoay có độ dài đường sinh bằng đường kính đáy và thể tích của khối trụ bằng $16\pi $ . Diện tích toàn phần của khối trụ đã cho bằng
Cho số phức z thỏa mãn ${{\left( 1-\sqrt{3}i \right)}^{2}}z=3-4i$. Môđun của z bằng:
Trong không gian Oxyz, cho hai mặt phẳng $\left( P \right):x-3y+2z-1=0,\,\left( Q \right):x-z+2=0$. Mặt phẳng $\left( \alpha \right)$ vuông góc với cả (P) và (Q) đồng thời cắt trục Ox tại điểm có hoành độ bằng 3. Phương trình của $\left( \alpha \right)$là:
Cho các số phức $z=-1+2i,\,\text{w}=2-i$. Điểm nào
trong hình bên biểu diễn số phức $z+\text{w}$?
.png)
Cho k,n là các số nguyên dương bất kì. Mệnh đề nào sau đây đúng?
Phương trình $\log \left( x+1 \right)=2$ có nghiệm là:
Tất cả các nguyên hàm của hàm số $f\left( x \right)={{3}^{-x}}$ là:
Cho hàm số $y=f\left( x \right)$có đồ thị như hình vẽ bên.
Mệnh đề nào sau đây đúng về hàm số đó?
.png)
Giả sử $f\left( x \right)$ là một hàm số bất kỳ liên tục trên khoảng $\left( \alpha ;\beta \right)$ và $a,b,c,\,b+c\in \left( \alpha ;\beta \right)$. Mệnh đề nào sau đây sai?
Cho hàm số $y=f\left( x \right)$ liên tục trên $\left[ -3;3 \right]$ và có bảng xét dấu đạo hàm như hình bên. Mệnh đề nào sau đây sai về hàm số đó?
.png)
Trong không gian Oxyz, mặt phẳng (P) đi qua điểm $M\left( 3;-1;4 \right)$ đồng thời vuông góc với giá của vectơ $a\left( 1;-1;2 \right)$ có phương trình là
Đường cong ở hình bên là đồ thị của hàm số nào dưới
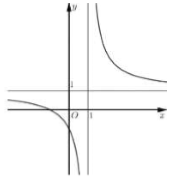 đây?
đây?
Cho cấp số nhân $\left( {{u}_{n}} \right)$, với ${{u}_{1}}=-9,\,{{u}_{4}}=\frac{1}{3}$. Công bội của cấp số nhân đã cho rằng
Trong không gian Oxyz, cho $E\left( -1;0;2 \right)$ và $F\left( 2;1;-5 \right)$. Phương trình đường thẳng EF là
Giả sử a, b là các số thực dương bất kỳ. Biểu thức $\ln \frac{a}{{{b}^{2}}}$ bằng
Trong không gian Oxyz, cho $a\left( -3;4;0 \right)$ và $b\left( 5;0;12 \right).$ Côsin của góc giữa a và b bằng
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với Ab = 3a, BC = a, cạnh bên SD = 2a và SD vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng
Cho hình hộp chữ nhật ABCD. A 'B 'C 'D ' có AB = a, AD = AA’ = 2a. Diện tích của mặt cầu ngoại tiếp hình hộp chữ nhật đã cho bằng
| 1 |
heyitsmekris97
Trần Nghĩa
|
18/50
|
| 2 |
trunghuyenlq
trung huyen
|
15/50
|
| 3 |
meongungocbaka
Mạc Nhiên
|
15/50
|
| 4 |
khonganbiet91
phạm hữu dương
|
8/50
|
| 5 |
tuandungitcn6
Nguyen Tuan Dung (JV)
|
1/50
|
Đề thi thử THPT môn Toán Chuyên ĐH Vinh lần 1 2019
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm